Dreier- und Vierervektoren

mechan. und relativistische Grundlagen - Dreier- und Vierer-Vektoren

In der klassischen Mechanik bestehen Orts- und Impulsvektoren aus drei Komponenten, entsprechend den drei Raumrichtungen, x, y, und z. Man nennt diese Vektoren daher auch Dreier-Vektoren:

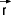(Dreier-)Ortsvektor: = (x, y, z)
(Dreier-)Impulsvektor: 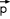= (p_x, p_y, p_z)

In der relativistischen Mechanik sind Ort und Impuls mit der Lichtgeschwindigkeit bzw. der relativistischen Gesamtenergie E verknüpft. Es ist daher naheliegend, den Ortsvektor um eine vierte Komponente "c^.t" zu erweitern. Wir verwenden für den Vierer-Ortsvektor den Buchstaben r:

Vierer-Ortsvektor: r = (x, y, z, c^.t)

Ein weiteres wichtiges Beispiel für einen Vierer-Vektor ist der Vierer-Impulsvektor. Um die Abhängigkeit des relativistischen Impulses von der relativistischen Gesamtenergie E zu berücksichtigen, wird als vierte Komponente E/c gewählt:

Vierer-Impulsvektor: p = (p_x, p_y, p_z, E/c)

Wir haben bereits die Gleichungen für die Lorentztransformation kennengelernt. Im Zusammenhang mit den Vierer-Vektoren ist es wichtig zu erwähnen, dass die Länge des Vierer-Ortsvektors invariant (d.h. unverändert) bei einer Lorentztransformation bleibt. Man beachte dabei, dass es sich hier nicht um einen euklidischen Raum handelt, und bei der Berechnung der "Länge" definitionsgemäß negative Vorzeichen

auftauchen. Die Länge l (der Einfachheit halber schreibt man deren Quadrat l²) ist dabei definiert als:
l²= r² = - x²- y²- z²+ c^2.t²
Setzt man die Gleichungen der Lorentztransformation ein (siehe rechts), so bleibt die Länge unverändert, d.h. man erhält:
l²= r² = - x²- y²- z²+ c^2.t² = - x'²- y'²- z'²+ c^2.t'² = r'² = l'² oder kurz: r²= r'²

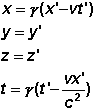
Die Gleichungen der Lorentztransformation (Raum-Zeit)

Die Länge des Vierer-Ortsvektors ist also bezüglich aller Koordinatensysteme gleich!

Auch der Betrag des Vierer-Impulsvektors (p²) ist eine invariante Größe bezüglich einer Lorentztransformation. p² ist folgendermaßen definiert:
p² = - p_x²- p_y²- p_z²+ E²/c²=
-

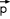²+ E²/c²= E₀²/c²
Die Größe E₀²/c² (Ruheenenergie) hat

bezüglich aller Koordinatensysteme denselben Wert.
Es gilt also auch hier: p² = p'². Man kann dies analog zum Ortsvektor zeigen, indem man die Gleichungen der Lorentztransformation für Impuls und Energie (siehe rechts) einsetzt (was hier allerdings zu weit führen würde).

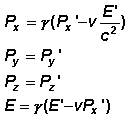
Die Gleichungen der Lorentztransformation für Impuls und Energie

Der Betrag des Vierer-Impulsvektors ist also bezüglich aller Koordinatensysteme gleich!

(siehe dazu auch:

)