Grundlagen der QM - Die Wahrscheinlichkeitsdichte |Y(x, t)|2 Entscheidend für die Interpretation der Wellenfunktion Y(x, t) ist die Wahrscheinlichkeitsdichte oder Wahrscheinlichkeitsverteilung |Y(x, t)|2  Was kann man sich unter einer Funktion, die die Wahrscheinlichkeitsdichte eines quantenmechanischen Zustands in Abhängigkeit von Ort x und Zeit t angibt, vorstellen? 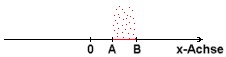Dazu betrachten wir am besten folgendes "eindimensionale Beispiel": Stellen wir uns eine beliebige Ortsachse vor, z.B. die x-Achse. Auf ein Stück der x-Achse zwischen den Werten A und B (mit A < B) prasseln - völlig gleichverteilt - rote Farbtropfen nieder, so dass dieses Stück schon ganz rot gefärbt ist.  Wir suchen eine Funktion, die uns folgende Frage "beantwortet": "Mit welcher Wahrscheinlichkeit trifft der nächste Tropfen einen Punkt irgendeines Intervalls [x1; x2] auf der x-Achse?" Wir können uns ganz sicher sein, dass Folgendes gilt: a) Wenn x1 = - ¥ und x2 = + ¥ ist, muss die Antwort "1" lauten, denn zwischen - ¥ und + ¥ trifft der nächste Tropfen ganz sicher. b) Wenn man x1 = A und für x2 genau die Mitte zwischen A und B wählt, muss die Antwort 1/2 lauten, denn in die Hälfte der roten Strecke wird der Tropfen mit der Wahrscheinlichkeit 1/2 treffen. 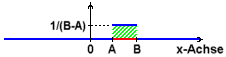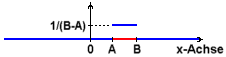Die allgemeine Lösung des Problems kann mit folgender Funktion F bestimmt werden  F(x) = 1/(B - A)    für x Î[A; B] und  F(x) = 0                 für x Ï [A; B]     wobei (B - A) die Länge der roten Strecke ist (siehe Abb.). Die Funktion F ist so gewählt, dass die Wahrscheinlichkeit dafür, dass der nächste Tropfen in das Intervall [x1; x2] trifft, der Flächeninhalt zwischen dem Graphen von F (blau in Abb. rechts) und dem  Intervall [x1; x2] auf der x-Achse ist. Der Flächeninhalt über einem Intervall auf der x-Achse ist hier sehr einfach zu berechnen, da es sich immer um ein Rechteck handelt. Der gesamte Flächeninhalt (grün schraffiert) hat den Wert 1, denn 1/(B - A) . (B - A) = 1. Die Wahrscheinlichkeitsdichte |Y(x, t)|2 ist nun nichts anderes als die Funktion F: |Y(x, t)|2 = F(x, t) Da in unserem Beispiel die Funktion F unabhängig von der Zeit t war, konnten wir an Stelle von F(x, t) kurz F(x) schreiben. In der QM verwendet man für die Wahrscheinlichkeitsdichte den Buchstaben r. Man scheibt: r(x, t) = |Y(x, t)|2 Wir haben in unserem Beispiel neben der Zeitunabhängigkeit noch zwei vereinfachende Voraussetzungen gemacht, die normalerweise nicht gelten.  1. Der Flächeninhalt unter dem Graphen der Wahrscheinlichkeitsdichte (Gr) ist höchst selten so einfach zu berechnen wie im Fall unseres Rechtecks. Normalerweise ist |Y(x, t)|2 keine so leicht veranschaulichbare Funktion, so dass man zur Bestimmung des Flächeninhalts (Abb. rechts, grün schraffiert) das Integral von x1 nach x2 berechnen muss. Diese Berechnung kann ausgesprochen schwierig sein. 2. Unser Beispiel ist ein eindimensionales Problem, üblicherweise sind alle drei Raumrichtungen zu betrachten. Das ist nicht weiter schlimm, denn das Prinzip der Berechnung bleibt gleich. r(x, t) = |Y(x, t)|2 ist nun eine Funktion in drei Dimensionen, wobei x zum dreidimensionalen Ortsvektor (x, y, z) wird. Das Integral zur Berechnung der Aufenthaltswahrscheinlichkeit muss nun über drei Raumrichtungen (òdx dy dz), also ein Volumen (òdV), berechnet werden. 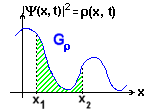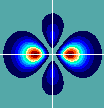Ein typisches Beispiel ist die Wahrscheinlichkeitsdichte verschiedener Anregungsstufen des Wasserstoffatoms. Die Abbildung rechts zeigt einen Schnitt durch die dreidimensionale Darstellung dieser "Dichte-Funktion". Verschiedene Farben entsprechen dabei den verschieden großen Aufenthalts- wahrscheinlichkeiten des Elektrons in den Teilgebieten. Außerhalb der "Keulen" ist das Elektron nur "sehr selten" anzutreffen. In der Chemie nennt man diese Darstellung ein Wasserstoff-Orbital-Modell.  Wir können zusammenfassen: Der quantenmechanische Zustand eines Teilchens wird durch die Wellenfunktion Y(x, t) beschrieben. Die Wahrscheinlichkeitsdichte |Y(x, t)|2  ist die Funktion, deren Integral über ein Volumen V die Aufenthaltswahr- scheinlichkeit dafür ist, dass sich das Teilchen zum Zeitpunkt t in V aufhält. Die Wahrscheinlichkeit, dass sich ein Teilchen des quantenmechanischen Zustands Y(x, t) im Volumen V aufhält ist:  ò | Y(x, t)|2 dV  Das Integral über den ganzen Raum (V¥) hat immer den Wert 1, denn die Wahrscheinlichkeit, dass das Teilchen "irgendwo" ist, ist 1. Man schreibt dafür kurz: ò |Y(x, t)|2 dV¥ = 1        Diese allgemeingültige Aussage nennt man Normierung.