Die schwache Wechselwirkung - Die Paritätsverletzung  Eine weitere Eigenschaft der schwachen Wechselwirkung unterscheidet sie deutlich von der starken und elektromagnetischen Wechselwirkung: Schwache Prozesse verletzen die sogenannte Raumspiegelungs- Symmetrie (Raumumkehrsymmetrie bzw. Parität). 1924 begründete der Physiker Wigner die Tatsache, dass ein Atom mindestens zwei Anregungszustände besitzt, mit der Invarianz der beschreibenden Wellenfunktion Y bezüglich der sogenannten Raumumkehr (Paritätsoperation).  Was bewirkt die Paritätsoperation bzw. Raumumkehr? Bei der Paritätsoperation wechseln alle Koordinaten ihr Vorzeichen. Das entspricht geometrisch einer Punktspiegelung am Ursprung.  Ein Punkt mit den Koordinaten (x, y, z) wird zu (-x, -y, -z). Geschwindigkeits- und Impulsvektoren drehen sich um. Der Windungssinn einer Schraube, die sog. Helizität, dreht sich um. Aus einer Rechts- wird eine Linksschraube. Allgemein: Polare Vektoren (üblicherweise nur als Vektoren bezeichnet) ändern ihr Vorzeichen. Manche Größen (r, p und L bezeichnen Vektoren!) bleiben aber auch gleich, z.B. der Drehimpuls L = r x p. Er ist das Vektorprodukt des Orts- und Impulsvektors (r und p). Da r und p ihre Vorzeichen ändern, bleibt das Produkt gleich. Der Drehimpulsvektor bleibt also unter der Paritätsoperation unverändert. Da der Spin eines Teilchens als Eigendrehimpuls interpretiert werden kann, bleibt auch er unverändert.   Allgemein: Axiale Vektoren bleiben unverändert.  In der Physik galt bis 1956 folgendes Prinzip (Paritätsinvarianz): Naturgesetze sind bezüglich der Paritätsoperation invariant. Das bedeutet, dass ein physikalischer Prozess auch dann gleich bleibt, wenn die Paritätsoperation durchgeführt wird, d.h der raumgespiegelte Prozess betrachtet wird. Man sollte also einen Prozess von seinem raumgespiegelten "Partner" nicht unterscheiden können. Für die elektromagnetische und starke WW gilt die Paritätsinvarianz. Folgendes Experiment von Wu, Ambler, Hayward, Hoppes und Hudson aus dem Jahr 1957 zerstörte allerdings den Glauben der Physiker an die Paritätsinvarianz bei der schwachen Wechselwirkung  Das Experiment von Wu et al.:  Kobalt-60 (60Co) ist ein b--Strahler, er emittiert also Elektronen. Aus der Paritätsinvarianz folgt, dass die Zählrate für emittierte Elektronen in eine Richtung parallel zum Kernspin genauso groß sein sollte, wie die in die entgegengesetzte. 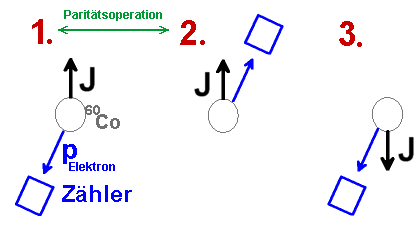In rechter Abbildung ist das Prinzip des Experiments dargestellt, die 60Co-Probe ist polarisiert.   zu 1.:  Die Kernspins (J) sind nach oben ausgerichtet. Der Zähler registriert die emittierten Elektronen mit dem Impuls pElektron. Nun wird die Paritätsoperation durchgeführt. Die raumgespiegelte Situation zeigt die 2. Skizze.   zu 2.:  Durch die Paritätsoperation drehen sich alle polaren Vektoren (hier nur pElektron) um. Der axiale Vektor J bleibt unverändert. Der Zähler müsste, wenn der Prozess der Elektronenemission invariant gegenüber der Paritätsoperation ist, die gleiche Zählrate liefern, wie bei 1..  zu 3.: In dem Experiment von Wu hat man aus experimentellen Gründen zum Vergleich mit 1. nicht den 2. Aufbau benutzt, sondern einfach die Kernspins J entgegengesetzt ausgerichtet. So konnte derselbe Zähler verwendet werden. Man beachte, dass 2. und 3. zwar um 180° gedreht, prinzipiell aber identisch sind. Das Ausrichten der Kernspins erfolgte durch ein starkes Magnetfeld B, zum Umdrehen der Kernspins musste es nur umgedreht werden (Bâ bei 1. und Bá bei 3.; die Kernspins richten sich entgegen dem äußeren Magnetfeld aus, vergleiche die beiden Abb. o. und u.).  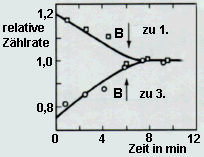Das Ergebnis war für viele Physiker niederschmetternd. Die Zählrate von 1. war deutlich höher als die von 3.. Die Polarisierung der 60Co-Kerne erforderte, dass die 60Co-Probe auf 0,01 K abgekühlt wurde. Da sie sich langsam "erwärmte", verlor die Probe an Polarisierung, so dass sie nach wenigen Minuten unpolarisiert war. Die relative Zählrate (Quotient aus Zählrate (polarisiert) und Zählrate (unpolarisiert)) geht daher im Diagramm gegen den Wert 1 (siehe Abb. rechts).   Entscheidend ist, dass die Zählraten im polarisierten Zustand (zu Beginn der Messung) unterschiedlich waren. Das war ein schlagender Beweis für einen Prozess, der nicht invariant gegenüber der Paritätsoperation ist. Man spricht daher von Paritätsverletzung Mittlerweile gibt es eine Reihe weiterer Beispiele für die Paritätsverletzung bei schwachen Wechselwirkungen. 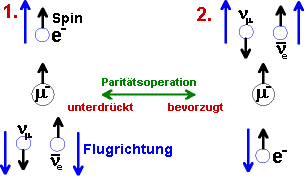Eines ist der Zerfall des Müons:    m- à nm + e- + ne  Die Müonen werden polarisiert und man untersucht, in welche Richtung die Elektronen emittiert werden. Falls die Paritätsinvarianz gilt, müssen in zwei entgegengesetzte Richtungen gleich viele Elektronen emittiert werden.   Im Experiment zeigt sich aber, dass die Elektronen bevorzugt entgegen ihrer Spinrichtung emittiert werden.   Die Leptonen besitzen alle den Spin 1/2. Die Spins der Neutrinos sind entgegengesetzt ausgerichtet (â und á), sie heben sich also auf. Aufgrund der Spinerhaltung muss das emittierte Elektron die gleiche Spinrichtung wie das Müon besitzen (hier beide á). In der Abb. links sind die beiden möglichen Szenarien dargestellt. Die Paritätsoperation dreht wieder die Flugrichtungen (polare Geschwindigkeits- vektoren) um, lässt aber die Spins (axiale Vektoren der Eigendrehimpulse) unverändert. Der 2. Zerfall, bei dem die Elektronen- flugrichtung entgegengesetzt zum Spin ist, das Elektron also linkshändig ist, wird bevorzugt. Der 1. Zerfall mit dem rechtshändigen Elektron ist unterdrückt. Diese Unsymmetrie zwischen rechts und links stellt die Paritätsverletzung dar. (siehe dazu  und  )