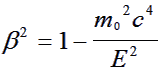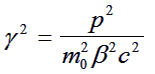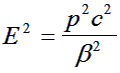So momentum becomes:

	(3a)
	(3b)

The energy of the particle becomes:

Square the Lorentz factor to give:

Rearrange (4) to give:
     

(6)

Square (6) and substitute it into (5). Rearrange the result to get:   

Rearrange and square (3) to get:   

Square (3) and then substitute (8) into it and simplify to get:  

Finally, substitute (7) into (9) and after some rearrangement the result below is obtained.

(10)

* ** *** ** *

As an aside.... Can you also show that, when beta becomes much less than 1, this reduces to the non-relativistic form: 

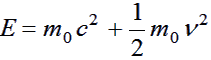
(11)

To do this start with equation (2) in the form:

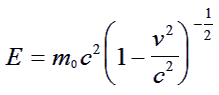(12)

Apply a binomial expansion to the term in the bracket and then apply the approximation that c>>v to remove unwanted terms.

NB. Binomial Expansion: This is a standard bit of maths that helps with some Physics problems. If you need help with it then ask a teacher or try a decent further maths textbook. 

For  -1 > x < +1
   

   
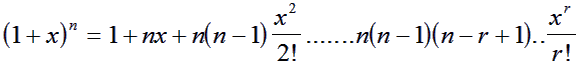
Where r! is factorial r. ( 3!=3*2*1=6). Because x is fractional terms in higher powers of r gradually become less and less significant and can be ignored.

  
Close