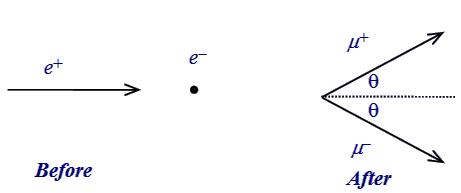
The incident positron (e⁺) has momentum p_e and total energy E_e and collides with a stationary electron (e^-) thereby annihilating to produce a 'virtual photon'. The virtual photon materialises into a new e⁺ and e^- pair or any other heavier particle antiparticle pair, such as μ⁺ and μ^-, provided sufficient energy is available. The μ⁺ and μ^- pair must have total momentum equal to p_e in order to conserve momentum in the collision.
  
We make a simplification and assume the pair are created with equal momenta and at the same angle to the positron direction (see Figure above). (This simplification does not affect our final conclusions).

Conservation of momentum in the positron direction gives:

	(1a)
	(1b)

At the positron beam energy which is just sufficient to create a μ⁺ and μ^-, pair (threshold energy), theta equals zero degrees. The particles then emerge moving in the same direction as the positron beam with momentum:

(2)

Now let’s see what conservation of total energy gives. The total energy before a collision is E_e+m_ec² because the target is stationary and possesses only its mass energy. The total energy of each μ⁺ and μ^- is the same because they have equal momentum. We then have

	(3a)
	(3b)

But we must satisfy the relativistic relation between total energy and momentum for each particle:

	(4a)
we get after some rearrangement:	(4b)
	(4c)
	(4d)
	(4e)

Therefore:

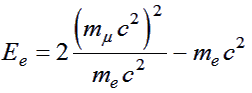(5)

  
Close