Because the K0 travels at speeds (v) approaching that of light, its properties are affected according to special relativity. Its mean decay time τ, as measured by us in the (stationary) laboratory, is lengthened by the Lorentz factor,
| |
(1) |
where,
| |
(2) |
Hence, the K0 mean lifetime becomes,
| |
(3) |
The mean distance travelled in the laboratory by the K0 is equivalent to its mean decay length, L, which can now be expressed as,
|
|
(4) |
Using equation (3) this becomes,
| |
(5) |
With,
| |
(6) |
we can rewrite equation (5) as,
| |
(7) |
rearranging equation (7) gives,
| |
(8) |
You can use equation (8) to calculate the mean decay time , using your value for L. However we also need to determine the Lorentz factor, γ: In the annihilation the K0 takes half of the available energy; which is equal to the incident beam energy E. Therefore, for the K0, can be determined using equations (9) and (10) for the energy of a particle travelling at relativistic speeds.
| |
(9) |
| |
(10) |
where mK is the K0
rest mass which you determined in the first part of the exercise, c
is the speed of light and the value of E, you chose
yourself.
Lets do an Example:
Remember, mKc2
= 0.497 GeV. If E is set at 10GeV then
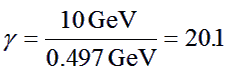 |
(11) |
If your length measurements give a mean decay
length L = 0.933m,
then we can now calculate τ
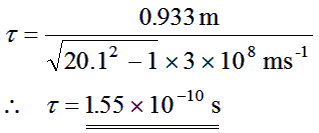 |
(12) |
This is close to the 'book' value given below. By taking more
length
measurements
you may obtain a better estimate.
Neutral kaon mean decay time (τ) = 0.89x10-10s