The mass of the K⁰ is given by the squares of its total energy

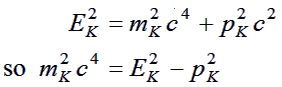(1)

We determine E_K and p_K from the energy and momentum of the π⁺ and π^- pair. Therefore

(2)

i.e. simple addition of the pion energies. The total momentum squared (p_K²) can be calculated by applying the cosine rule to the triangle of vectors shown below where p₁ and p₂ are the respective pion momenta.
   

      
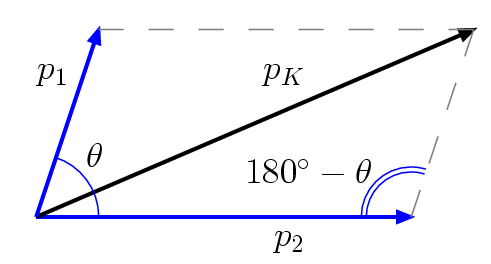
Equivalent to...   
     

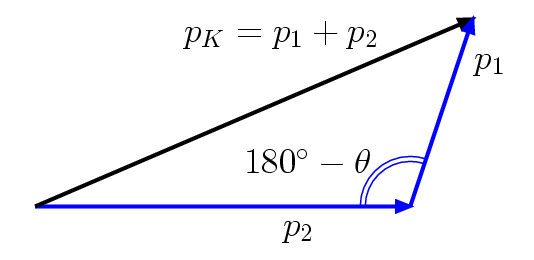
Hence,

(3)

so that,

(4)

Expand this equation and rearrange. Remember that,

(5)

Show that,

(6)

  
Close