Measurements are made by positioning the mouse pointer on a particle track and clicking the left-hand mouse button; a circle will be drawn at this point and its centre co-ordinates stored by the computer. Repeat this procedure three times to display three circles. The computer will then display, in a data box, the radius of curvature (in meters) of a circle which lies through these three points (remember three points uniquely define a circle). If you have chosen your points carefully they should lie, equally spaced, on the particle track and the displayed radius value should correspond to the radius of the particle track. It is up to you to position the Radius circles correctly, poor positioning will result in an inaccurate value for r making it difficult, if not impossible, to determine the particle's rest mass.
There are two ERROR! dialogue boxes that can appear when you are placing your Radius points. If your points are too close together then an error box appears, telling you to try again, this time spacing your points evenly along the track to obtain a more accurate value for your radius. If you have chosen a large incident beam energy then the particle tracks can often appear as straight lines and your points may lie in a line, giving an infinite radius of curvature! If this happens an error box will appear, advising you to try again on a new particle track, this time with a lower beam energy and/or a larger magnetic field strength. Either way this should produce a track that is more curved - can you see why? Increasing the magnetic field increases the force which pushes the charged particles into a circular path. Reducing the beam energy reduces the new particles linear momentum and so, according to equation (1), the radius of curvature is reduced.
| |
(units: GeV/c) |
(1) |
Even when you have placed your points
correctly, it is still advisable to repeat the measurements on the same
particle track, in order to obtain a mean radius for the same incident
beam energy and magnetic field settings. To start a new measurement,
position and click the mouse a fourth time, this will then become the
first point of a new Radius measurement and the previous points will be
erased automatically. Select a further two points, so that you again have
three circles, and the new radius value will be displayed in the data box.
Make a note of your r values each time and calculate a mean.
Hints: generally, to obtain the best results select: Incident beam energy
(E) = 1GeV, Magnetic field strength (B) = (1 or 2) T and take
three or
more Radius measurements on the same particle track. As discussed above if
E is too large the radius is too large, while if B is too large the radius
will be too small making radius measurements, in both instances,
inaccurate. With practice you will find suitable settings which result in
reliable particle identification from their rest masses.
How does the computer work out the radius?
When you click the mouse a pair of x,y coordinates are returned. Three sets of x,y coordinates are sufficient to define a circle.
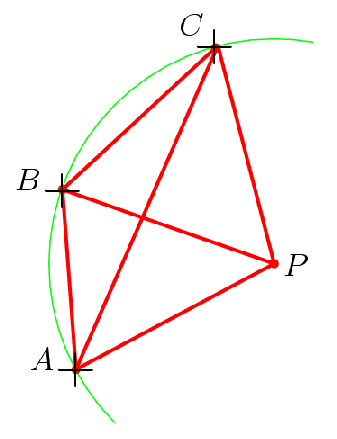
AP = BP = CP = radii of the circle.
The machine applies Pythagoras theorem to pairs of the coordinates pairs to calculate AB, AC and BC.
The cosine rule is then applied to
ΔABC
in order to calculate ![]() ABC.
ABC.
ΔBAP and
ΔBCP are both isocoles. This can
be used to show that:
![]() ABC =
ABC =
![]() BCP +
BCP + ![]() BAP.
BAP.
Thus ![]() APC = 360 - 2
APC = 360 - 2![]() ABC
ABC
The cosine rule is now applied to ΔACP to find the radius of the circle.