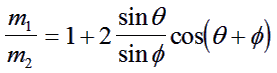Momentum and Angles for Hard Sphere Collisions.

   m₁ = mass of incident (blue) ball.

   m₂ = mass of target (red) ball.

   u₁ = initial velocity of incident ball.

   v₁ = final velocity of incident ball.

   v₂ = final velocity of target ball. 

Remember that the target ball is stationary and so has zero initial velocity.

Use the equation for energy conservation.

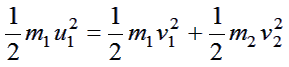
(1)

and rearrange it to give   

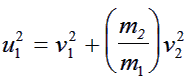(2)

Now consider the three momentum vectors in the system.
  
  
   
These can be redrawn to form a closed triangle.
   
  

      
There are three distinct cases that apply to this triangle of momentum vectors.

Now apply the cosine rule to the momentum vector triangle.   

(3)

Consider Case 2 first ( because it is easiest!).  cos C = 0.  For this case equation (2) rearranges to give:     

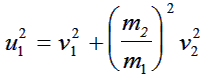(4)

Comparing this equation with equation (2) gives:

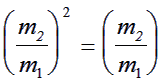(5)

This can only be true when the masses of the spheres are identical. 

Thus if an experiment yields θ+Φ = 90⁰ then this shows that the incoming and target particles have identical masses.

Now consider case 1 remembering that CosC is negative.  This allows equation (3) to be transformed into the inequality:   

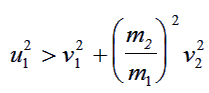(6)

Comparing this with equation (2) yields:

(7)

This can only be the case if m1 > m2. 

Thus if an experiment yields θ+Φ < 90⁰ then this shows that the incoming particle has more mass than the target particle.

Now consider case 3 remembering that CosC is positive.  This allows equation (3) to be transformed into the inequality:
   

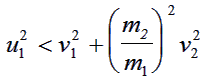(8)

Comparing this with equation (2) yields:

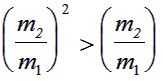(9)

This can only be the case if m₁ < m₂. 

Thus if an experiment yields θ+Φ > 90⁰ then this shows that the incoming particle has less mass than the target particle.

If you enjoy a challenge then you can derive the formula that links m₁, m₂, θ and Φ.  You need to use energy, momentum in horizontal and vertical directions and the cosine rule to set up some simultaneous equations that can then be reduced using standard trig identities to the equation.

  
Close