mechan. und relativistische Grundlagen - Masse, Geschwindigkeit und Beobachter   Gedankenexperiment: Angenommen man bewegt sich mit einer Geschwindigkeit von 90% der Lichtgeschwindigkeit, also mit v =  0,9.c und misst gleichzeitig mit einer mitgeführten Waage seine Masse. Stellt man dann eine höhere Masse als in Ruhe fest? Wie hängt die relativistische Masse mit der Geschwindigkeit zusammen?  Man muss hierbei zwischen zwei sogenannten Bezugssystemen unterscheiden, dem Ruhesystem des bewegten Körpers  und dem System, in dem sich der Beobachter in Ruhe befindet (Laborsystem).   Eine sich schnell bewegende Person stellt in dem mitbewegten System (ihrem Ruhesystem) immer die gleiche Masse wie in Ruhe fest. Dies ist leicht verständlich, wenn man folgendes weitere Gedankenexperiment durchführt:   Nehmen wir an, auf der Erde steht eine Person auf einer Waage, die gerade 75 kg anzeigt. Ein Beobachter bewegt sich währenddessen mit 0,3.c auf die Erde zu, ein anderer mit 0,6.c. Die beiden Beobachter sehen also die Erde mit unterschiedlichen Geschwindig- keiten auf sich zu rasen. Beide würden als Masse des Menschen auf der Waage unterschiedliche Massen angeben. Die Waage auf der die Person steht, kann aber natürlich nicht zwei verschiedene Werte gleichzeitig anzeigen. Sie - da sie sich mit dem beobachteten Menschen mitbewegt - zeigt immer seine Ruhemasse (75 kg) an. Die Masse eines Körpers bleibt in seinem Ruhesystem immer gleich. Von einem anderen System aus, an dem sich das Ruhesystem des Körpers schnell vorbeibewegt, stellt man die relativistische, also höhere Masse m fest. Man nennt die relativistische Masse auch bewegte oder dynamische Masse. Beispiel:   Betrachten wir Elektronen im Speicherring HERA bei DESY. Sie haben eine Ruhemasse m0 von 511 keV/c2  und eine Gesamtenergie von 30 GeV. Ihre Geschwindigkeit beträgt 0,9999999998.c. Könnten sie selbst ihre Masse feststellen, würden sie nach wie vor nur 511 keV/c2 messen.   Um sie auf die Kreisbahn im Speicherring zu zwingen, verwendet man Magnetfelder. Die Stärke des Magnetfeldes hängt dabei von der Masse und Geschwindigkeit der Teilchen ab. Da die Magnete ruhen und sich die Elektronen mit "fast c" an ihnen vorbeibewegen, besitzen die Elektronen für sie eine relativistische Masse m. m beträgt bei dieser Geschwindigkeit ca. das 58709-fache von m0, nämlich 30 GeV/c2. Für einen außenstehenden Beobachter (also auch die Magnete) sind die Elektronen 58709-mal so schwer wie in Ruhe (m/m0 = 58709)! Das Magnetfeld muss dementsprechend stärker gewählt werden! 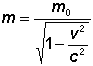Der genaue Zusammenhang zwischen relativistischer Masse m und Geschwindigkeit v lautet:    Der Faktor v/c wird meist mit b abgekürzt: b = v/c. Sehr hohe Geschwindigkeiten gibt man in "Vielfachen der Lichtgeschwindigkeit" an, z.B. v = 0,5.c. In diesem Fall ist also b = 0,5.  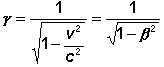Den Kehrwert der Wurzel in der Beziehung zwischen m und m0 bezeichnet man mit  g:         Man erkennt, dass b für v à c gegen 1 geht und g à ¥.  Mit dieser Abkürzung g vereinfacht sich der Zusammenhang zwischen relativistischer Masse und Ruhemasse zu m = m0. g.  Mit m = m0. g erkennt man, dass gilt:    m à ¥   für   v à c.  Nähert sich die Geschwindigkeit eines Körpers der Lichtgeschwindigkeit c, wird seine relativistische Masse m immer größer. Im Grenzfall v à c ist die relativistische Masse m à ¥. Der Zusammenhang zwischen relativistischer Masse und Ruhemasse ist lautet:   m = m0. g  Neben einem Massenzuwachs stellt ein ruhender Beobachter bei einem sehr schnell bewegten Körper noch eine weitere "Besonderheit" fest: Für den bewegten Körper vergeht die Zeit langsamer! Mehr dazu auf der nächsten Seite.