mechan. und relativistische Grundlagen - Lorentztransformation  Die Zeitdilatation hat gezeigt, dass die Zeitmessung, z.B. die Messung der Lebensdauer der Müonen, von der Geschwindigkeit abhängt, mit der sich Beobachter und "beobachteter Gegenstand" relativ zueinander bewegen. Dieser Zusammenhang wird oft unter dem Stichwort "bewegte Uhren gehen langsamer" zusammengefasst. Wir betrachten nun folgende Situation:   Ein für uns ruhender Speicherring sei der Ursprung eines Koordinatensystems A mit den Koordinaten (x', y', z'). Seine Zeit ist mit t' bezeichnet.    In die x'-Richtung bewegt sich ein Müon mit der Geschwindigkeit v und mit ihm das Koordinatensystem B mit den Koordinaten (x, y, z) und der Zeit t.   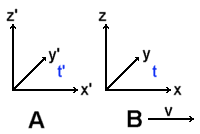Beim ersten Vorbeifliegen des Müons (B) am Koordinatenursprung von A sei der Zeitnullpunkt (t = t' = 0 bei x = x' =0), d.h. beide Uhren beginnen dort zu laufen. Wie hängen die sogenannten Raum-Zeit-Koordinaten von A (x', y', z', t') mit denen von B (x, y, z, t) zusammen?   Wir benutzen wieder die üblichen Abkürzungen:   b = v/c       und 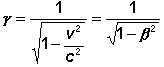Bezüglich A entfernt sich B mit der Geschwindigkeit v. Daher hat der Ursprung von B bezüglich A die Koordinaten:   x' = v.t'   y' = 0   z' = 0   Da sich B (der Einfachheit halber) nur in x'- bzw. x-Richtung bewegt, bleiben die anderen beiden Koordinaten identisch:   y = y'   z = z'   Zwischen x und x' gilt der Zusammenhang:   x = g(x' - v.t')   Für die beiden Zeiten t und t' gilt:   t = g(t' - v.x'/c2)   Man kann leicht alle Koordinaten vertauschen (t « t', ...), es muss dann nur v durch -v ersetzt werden!   Diese Gleichungen (siehe rechts) erlauben es, auszurechnen, welche Raum-Zeit-Koordinaten ein Ort, der bezüglich A die Raum-Zeit-Koordinaten (x', y', z', t') hat, bezüglich des Koordinatensystems B besitzt   (und umgekehrt). Man nennt die Überführung der Koordinaten eines Systems in das eines anderen Systems Lorentz-Transformation nach dem Physiker Lorentz.   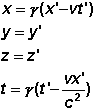Beispiel: Ein Teilchen (System B) bewegt sich, der Einfachheit halber in Richtung der x'- bzw. x-Achse mit v = 0,99.c an A vorbei und beide Uhren (A und B) beginnen zu laufen.    Welche Raum-Zeit-Koordinaten hat das Teilchen bzgl. A und B für die A-Zeit t' = 10-7 s?   Da es sich auf der x'-Achse bewegt ist y' = y = 0 und z' = z = 0. Da es sich mit v bewegt, hat es nach t' bzgl. A die x'-Koordinate x' = v.t' = 0,99 . 3.108 m/s . 10-7 s = 30 m (mit c = 3.108 m/s).    Im A-System ist das Teilchen also 30 m weit gekommen.   Und im B-System? Wir benutzen die Transformationsformel x = g(x' - v.t') und setzen x' = v.t' ein:  x = g(v.t' - v.t') = 0   Wir erhalten für die x-Koordinate (B-System) x = 0. Das ist leicht verständlich, denn das Teilchen befindet sich ja immer im Ursprung seines eigenen Koordinatensystems B. Man nennt daher B auch das Ruhesystem des Teilchens. Dies ist ein einfacher Sonderfall der Transformationsgleichungen.  Es fehlt noch die B-Zeit t. Dazu benutzen wir wieder eine Gleichung der Lorentztransformation:  t = g(t' - v.x'/c2) und setzen x' = v.t' ein:   t = g(t' - v.v.t'/c2) = g(t' - t'.v2/c2) = g(t' - t'.b2) = g(1 - b2).t' wir ersetzen nun nach obiger Angabe g und dann im letzten Schritt noch b. Daraus folgt: 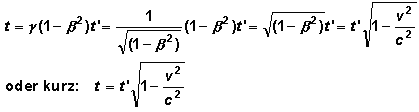   Wir erhalten als Ergebnis nichts anderes als die Formel der Zeitdilatation. Setzen wir t' = 10-7 s und v = 0,99.c ein, so erhalten wir t = 0,14.10-7 s. Während für den Beobachter in A 10-7 s vergehen, sind es für das Teilchen (in B) nur 14% dieser Zeitspanne, 0,14.10-7 s.  Neben den Gleichungen der Lorentztransformation für die Raum-Zeit kann man analog dazu Gleichungen für Energie und Impuls angeben. 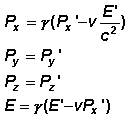Sie lauten: Wir haben in dieser Seite die sogenannten Raum-Zeit-Koordinaten, im Prinzip einen Vektor aus 4 Komponenten, verwendet. Diese Schreibweise eignet sich in der relativistischen Mechanik besonders gut. Auf der nächsten Seite gehen wir genauer darauf ein.