Streu-Experimente mit festem Target - Der Wirkungsquerschnitt (geometrische Interpretation)  Der Begriff Wirkungsquerschnitt kann auf verschiede Weisen interpretiert werden. Am anschaulichsten stellt man sich darunter die geometrische   Querschnittsfläche vor, die ein Target einem anfliegenden Teichen bietet, so dass beim Treffen des Teilchens in diese Fläche irgendeine Wirkung eintritt. Beispiel:   Bei starkem Regen steht jemand mit einem aufgespannten Regenschirm auf einem Fußballfeld. Die Tropfen prasseln auf den Schirm und das Feld. Wenn man als Wirkung das "Auftreffen eines Tropfens auf den Schirm" bezeichnet, so ist der Wirkungsquerschnitt des Schirms gleich der Fläche des aufgespannten Schirms.   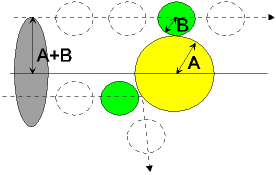Beispiel:   Viele kleine Kugeln mit Radius B fliegen auf eine große Kugel mit Radius A (das Target) zu. Eine Wirkung (Abprallen) tritt nur dann ein, wenn eine kleine Kugel durch die Kreisfläche mit Radius A + B fliegt (siehe Abbildung rechts, dunkelgraue Fläche). Der Wirkungsquerschnitt s des Targets wäre folglich bei "Beschuss" mit den kleinen grünen Kugeln s = (A + B)2p.   Wichtig!   Spielt bei makroskopischen Teilchenstößen noch die geometrische Form die wichtigste Rolle für die Größe des Wirkungsquerschnitts, so ist im Bereich der Elementarteilchen vor allem die Art der Wechselwirkung bzw. die Reichweite des Wechselwirkungs- potentials ausschlaggebend! Der Wirkungsquerschnitt hängt nicht nur vom Target sondern auch von der Art der Teilchen, mit denen "geschossen" wird, und ihren Eigenschaften (Energie, Ladung...) ab! 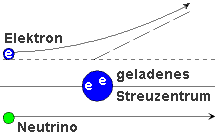Beispiel:   Für die Streuung von Neutrinos an einem geladenen Streuzentrum wird man sicher einen kleineren Wirkungsquerschnitt erhalten als bei Streuung von Elektronen am gleichen Zentrum (siehe Abbildung rechts oben). Das elektrisch ungeladene Neutrino fliegt unbeeinflusst am geladenen Streuzentrum vorbei, das geladene Elektron wird abgelenkt.  Ein weiteres Beispiel soll die anschauliche Betrachtung des Wirkungsquerschnitts bei der Coulomb-Abstoßung darstellen.