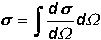
Streu-Experimente - Der (totale) Wirkungsquerschnitt bei Coulomb-Streuung  Wie groß ist der (totale) Wirkungsquerschnitt s bei Coulomb-Streuung, wie groß ist also die Fläche, bei der das Teilchen, wenn es durch sie fliegt, eine Ablenkung erfährt?  Allgemein ist der WQ s das Integral des differenziellen WQ ds/dW über alle Raumwinkelelemente dW:   Wir drücken wieder dW durch dq aus: dW = 2p sinq . dq   Da die Situation radialsymmetrisch ist, verursacht der Azimutwinkel f nur den Faktor 2p.   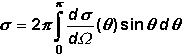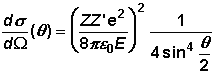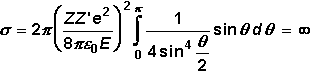Nun setzen wir den differenziellen Wirkungsquerschnitt ds/dW für die Coulomb-Streuung     ein, und müssen folgendes Integral berechnen:   Das Ergebnis ist bereits angegeben, s = ¥.  Es ist nach den Regeln leicht zu sehen, dass das Integral divergiert.  Dieses Ergebnis entspricht der Tatsache, dass die elektromagnetische Wechselwirkung eine unendliche Reichweite besitzt. Wir haben dies bereits an anderer Stelle besprochen . Wie erwähnt, findet strenggenommen immer Streuung statt, wenn auch bei verschwindend kleinen Streuwinkeln. In der Praxis ist aber die Ladung des Atomkerns von der Elektronenhülle abgeschirmt. 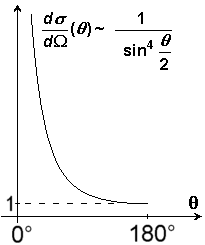Für sehr große Stoßparameter b muss die Streuwahrscheinlichkeit daher modifiziert werden. Das Integral ergibt dann einen endlichen Wert für den totalen Wirkungsquerschnitt.  Auf der nächsten Seite findet man zwei Messbeispiele von Wirkungsquerschnitten.