__________    Feynman-Kalkül - Dimension der Amplitude M 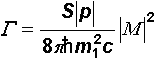    Der Zusammenhang zwischen Zerfallsrate G und Amplitude (siehe rechts) erlaubt uns die Einheit von M zu bestimmen. G hat die Einheit s-1. Fasst man die bekannten Einheiten der rechten Seite zusammen, so erkennt man, dass M die die Einheit eines Impulses (1 Ns) hat: [M] = [p] = 1 Ns (für Zerfall)  Für einen Drei-Körper-Prozess (das zugehörige Feynman-Diagramm besitzt also 3 äußere Linien) hat M die Einheit eines Impulses. 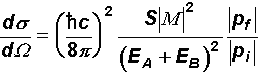 Auch die Formel für den differentiellen Wirkungsquerschnitt lässt eine Bestimmung der Einheit von M zu. Allerdings stellt man hier fest, dass M eine dimensionslose Zahl ist.   Für einen Vier-Körper-Prozess (das zugehörige Feynman-Diagramm besitzt also 4 äußere Linien) ist M eine dimensionslose Zahl.  Allgemein stellt man fest:  Die Amplitude M hat die Dimension "eines Impulses hoch 4 - n": [p4-n] = (1 Ns)4-n,  wobei n die Anzahl der äußeren Linien des zugehörigen Feynman-Diagramms ist.  Jetzt aber weiter zum Feynman-Kalkül und der genauen Bestimmung von M.