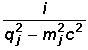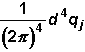Feynman-Kalkül
- Allgemeines Rechenschema zur Bestimmung
der Amplitude M
Im
Folgenden soll allgemein die Methode der Berechnung der Amplitude beschrieben
werden. Wir betrachten dazu das rechte Feynman-Diagramm (ohne innere Linien)
eines beliebigen Prozesses, dessen Amplitude M bestimmt werden soll.
Alle beteiligten Teilchen haben Spin 0.
Bei den
folgenden Ausführungen ist weniger die mathematische Durchführung (die
ist in der Realität beliebig schwierig!) wichtig, als das Verständnis
der groben Zielrichtung des "Rituals".
|
|
 Im
Prinzip wird die Amplitude M als Integral über das Produkt einzelner
Faktoren dargestellt und berechnet. Das Feynman-Kalkül beschreibt
in erster Linie das Aufstellen dieser Faktoren und die Berechnung
des Integrals. Im
Prinzip wird die Amplitude M als Integral über das Produkt einzelner
Faktoren dargestellt und berechnet. Das Feynman-Kalkül beschreibt
in erster Linie das Aufstellen dieser Faktoren und die Berechnung
des Integrals.
|
|
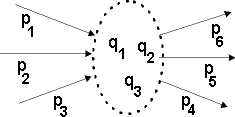
 1. Beschriftung:
1. Beschriftung:
Die
Vierer-Impulse  der äußeren Linien (p1,
p2, p3,
...) und inneren Linien (q1,
q2, q3,
...) werden nummeriert (siehe Abbildung rechts oben).
der äußeren Linien (p1,
p2, p3,
...) und inneren Linien (q1,
q2, q3,
...) werden nummeriert (siehe Abbildung rechts oben).
 2. Kopplungskonstante:
2. Kopplungskonstante:
Zu
jeder Wechselwirkung eines Vertex gehört ein Faktor g
~ 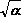 , wobei
a
die Kopplungskonstante
der zugehörigen Wechselwirkung bezeichnet. Für jeden Vertex wird
daher ein Faktor -ig (mit dem komplexen i) notiert. , wobei
a
die Kopplungskonstante
der zugehörigen Wechselwirkung bezeichnet. Für jeden Vertex wird
daher ein Faktor -ig (mit dem komplexen i) notiert.
 3. Propagator:
3. Propagator:
Für
jede interne Linie, d.h. für jedes virtuelle Teilchen, wird ein Faktor
der Form
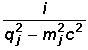 notiert.
Es sei angemerkt, dass es hier nur um die prinzipielle Form des Terms geht,
in exakten Berechnungen kann er wesentlich aufwendiger sein. Man nennt
ihn Propagator (-term). Wir gehen auf der nächsten Seite genauer
darauf ein. Entscheidend dabei ist, dass mj
und qj (Masse
und Viererimpuls des j-ten virtuellen Teilchens) quadratisch im
Nenner des Propagators eingehen. Sie bestimmen damit ganz entscheidend
den Betrag des Propagators und dadurch auch den Beitrag
der entsprechenden Wechselwirkung, die durch das Austauschteilchen (innere
Linie) vermittelt wird.
notiert.
Es sei angemerkt, dass es hier nur um die prinzipielle Form des Terms geht,
in exakten Berechnungen kann er wesentlich aufwendiger sein. Man nennt
ihn Propagator (-term). Wir gehen auf der nächsten Seite genauer
darauf ein. Entscheidend dabei ist, dass mj
und qj (Masse
und Viererimpuls des j-ten virtuellen Teilchens) quadratisch im
Nenner des Propagators eingehen. Sie bestimmen damit ganz entscheidend
den Betrag des Propagators und dadurch auch den Beitrag
der entsprechenden Wechselwirkung, die durch das Austauschteilchen (innere
Linie) vermittelt wird.
 4. Sicherung
der Energie- und Impulserhaltung:
4. Sicherung
der Energie- und Impulserhaltung:
Für
jeden Vertex kommt eine (Dirac`sche) Deltafunktion
(d(...))
folgender Form hinzu:
(2p)4
. d4(k1
+ k2 + k3
+ ...)
Die
k`s entsprechen den p1,
p2, p3,
..., wobei einlaufende p`s positiv und auslaufende negativ eingesetzt werden.
Die Deltafunktion hat u.a. die Eigenschaft, dass sie den Wert 0 annimmt,
wenn ihr Argument ungleich 0 ist. Hier wäre das der Fall, wenn die
Summe der einlaufenden Impulse nicht mit der der auslaufenden übereinstimmt.
Damit wird die Erhaltung von Energie und Impuls an jedem Vertex gesichert.
 5. Integration
über die internen Impulse qj:
5. Integration
über die internen Impulse qj:
Für
jede interne Linie wird ein Faktor der Form
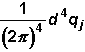 geschrieben
und über alle internen Impulse qj
integriert.
geschrieben
und über alle internen Impulse qj
integriert.
 6. Streichen
der enthaltenen Deltafunktion:
6. Streichen
der enthaltenen Deltafunktion:
Nach
der Integration wird der Term eine Deltafunktion der Form (2p)4
. d4(p1
+ p2 + p3
+ ... - pn) enthalten,
die über die Impuls- und Energieerhaltung "wacht". Sie wird jetzt
gestrichen. Der ganze Ausdruck ist gleich -iM zu setzen.
Was hier in wenigen Zeilen beschrieben wurde, kann für
komplexe Feynman-Diagramme höherer Ordnung, d.h. mit mehreren Vertices
bzw. vielen inneren Linien, sehr schnell sehr aufwendig werden. Zum genauen
Verständnis ist eine Auseinandersetzung mit entsprechender Literatur (z.B. ![zum Literaturverzeichnis [GRI 1996, 221]](../button_gifs/booksm.gif) ) )
|
unabdingbar. Für einen Einblick in die Technik des Feynman-Kalküls
soll uns diese Übersicht genügen. Auf den nächsten Seiten
werden wir dazu noch zwei Beispiele (Zerfall und Streuung) betrachten.
Zunächst aber kurz zu den Propagatoren.
|
|
|
 der äußeren Linien (p1,
p2, p3,
...) und inneren Linien (q1,
q2, q3,
...) werden nummeriert (siehe Abbildung rechts oben).
der äußeren Linien (p1,
p2, p3,
...) und inneren Linien (q1,
q2, q3,
...) werden nummeriert (siehe Abbildung rechts oben).
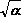 , wobei
a
die Kopplungskonstante
der zugehörigen Wechselwirkung bezeichnet. Für jeden Vertex wird
daher ein Faktor -ig (mit dem komplexen i) notiert.
, wobei
a
die Kopplungskonstante
der zugehörigen Wechselwirkung bezeichnet. Für jeden Vertex wird
daher ein Faktor -ig (mit dem komplexen i) notiert.