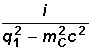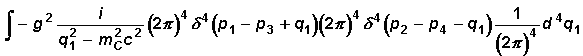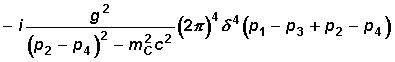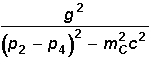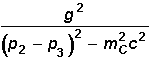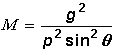Bestimmung der Amplitude M bei Zweikörperstreuung

Feynman-Kalkül - Bestimmung der Amplitude M bei Zweikörperstreuung

Wir betrachten die Zweikörperstreuung (A + A à B + B) in niedrigster Ordnung. Beiträge von Diagrammen höherer Ordnung lassen wir in diesem sehr vereinfachten Modell außen vor. Wir führen wieder die einzelnen Schritte des Feynman-Kalküls durch:

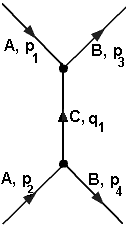
zwei A-Teilchen werden aneinander gestreut

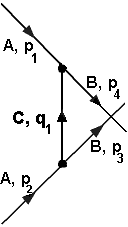
1. Beschriftung:
Die Impulse sind bereits in rechter Abbildung eingetragen. Es gibt eine innere Linie (C, q₁).

2. Kopplungskonstante:
Die beiden Vertices liefern zwei Faktoren -ig, also -g².

3. Propagator:
Der Propagator von C lautet: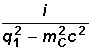

4. Sicherung der Energie- und Impulserhaltung:
Die Deltafunktionen für die Vertices lauten: (2p)^4
.d⁴(p₁ - p₃ + q₁) und (2p)^4
.d⁴(p₂ - p₄ - q₁)

5. Integration über den internen Impuls q:
Das Integral aller bisher aufgestellter Faktoren über den internen Impuls lautet:

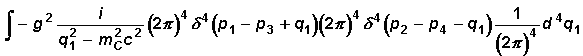Die Integration wird durch die Wahl des Punktes q₁ = p₂ - p₄vereinfacht und man erhält:

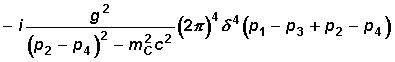
6. Streichen der enthaltenen Deltafunktion:
Die Deltafunktion wird gestrichen. Der restliche Ausdruck wird gestrichen und gleich -iM gesetzt. Man erhält für M:

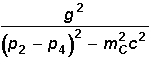Dies ist die Amplitude des oben dargestellten Prozesses der Ordnung g².

Damit ist man aber für den gesamten Streuprozess noch nicht am Ende. Es ist nämlich noch ein weiteres Diagramm der Ordnung g² des gleichen Prozesses möglich (siehe Abbildung rechts). Da sich dieses Diagramm nur durch die Vertauschung p₃ ßà p₄ von obigem unterscheidet, können wir M für diesen Prozess sofort angeben: 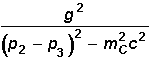Die gesamte Amplitude des Prozesses (Ordnung g²) ist einfach die Summe der beiden einzelnen: M = 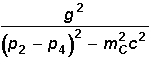+ 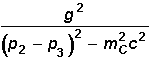Durch geometrische Überlegungen kann dieser Ausdruck noch umgeformt werden und in Abhängigkeit vom Streuwinkel und dem Anfangsimpuls p von Teilchen A (mit p₁) angegeben werden:
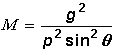
		Mit dieser Amplitude kann nun wiederum direkt der differentielle Wirkungsquerschnitt des Prozesses für die Ordnung g² berechnet werden. Amplitudenberechnungen für höhere Ordnungen mit 4 und mehr Vertices und entsprechend mehr inneren Linien werden extrem aufwendig, da die Anzahl der möglichen Feynman-Diagramme sehr schnell zunimmt. Man beachte wieder, dass es sich hier um eine Vereinfachung handelt. Zum vollständigen Verständnis ist eine Auseinandersetzung mit entsprechender Literatur notwendig. (siehe z.B. )