Grundlagen der QM - Vergleich von klassischer Mechanik und Quantenmechanik Die Mechanik, wie sie in der Schule behandelt wird, bezeichnet man als  klassische Mechanik (KM). Die Quantenmechanik (QM) stellt keine Erweiterung der klassischen Mechanik dar, sondern ist eine eigene, völlig neue Theorie, die dynamische Prozesse im mikroskopischen Bereich beschreibt. Dabei gilt das Prinzip, dass die Quantenmechanik die klassische Mechanik als Grenzfall für hohe Energien bzw. für den makroskopischen Bereich mit einschließt. Man nennt dieses Prinzip das Korrespondenzprinzip. Ein Vergleich zwischen den grundlegenden Forderungen und Annahmen der QM und denen der KM macht die neue Interpretation des Begriffs "Teilchen" deutlich. Wir vergleichen die Aussagen von QM und KM zur Determiniertheit (d.h. "ursächliche Vorbestimmtheit"). (siehe dazu auch  ) Klassische Mechanik (KM): In der KM sind alle Teilchen exakt durch die Größen Ort, Geschwindigkeit, Beschleunigung, Masse, Ladung, Energie und Impuls in ihrem zeitlichen Verhalten - der Raum-Zeit-Bahn - lückenlos vorbestimmt. Mit Messinstrumenten kann man diese Größen eines Teilchens (im Rahmen der Messgenauigkeit) beliebig genau angeben. Zur Betrachtung der Bewegungen genügt es oft, den von anderen Teilchen unabhängigen Schwerpunkt zu betrachten. Man kennt die wirkenden Kräfte und kann daher genau vorhersagen, welche Bahnkurve z.B. ein fliegender Ball beschreiben wird. Beispiel (KM): Ein Ball, der mit der Geschwindigkeit 1 m/s gerade durch eine offene Tür auf eine 2 m entfernte Wand zurollt, wird in 2 s an einer vorher bestimmbaren Stelle auf die Wand prallen. Die Raum-Zeit-Bahn ist in der klassischen Mechanik vorbestimmt! Quantenmechanik (QM): Die QM lässt keine Einzelbetrachtungen sondern nur statistische Aussagen zu. Es kann nicht mit absoluter Sicherheit vorhergesagt werden, wo sich z.B. ein Elektron im nächsten Augenblick befinden wird. Es gibt keine Raum-Zeit-Bahnen, schon gar keine vorbestimmten! Beispiel (QM): Ein Elektron fliegt gerade auf einen engen Spalt zu, hinter dem ein Schirm aufgestellt ist, auf dem auftreffende Elektronen schwarze Punkte verursachen. Was wird man auf dem Schirm beobachten? Antwort: "Einen schwarzen Punkt". An welcher Stelle? Antwort: "Unbekannt!". 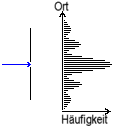Wenn viele Elektronen (z.B. ein Strahl) auf den Spalt treffen, werden sich die schwarzen Punkte nach einer bestimmten Häufigkeitsverteilung am Schirm anordnen (s. Abb. rechts), so dass zwar nie gesagt werden kann, wohin ein einzelnes Elektron fliegt, aber genau angegeben werden kann, mit welcher Wahrscheinlichkeit es in einen bestimmten Bereich trifft. Auch die ringförmige Schwärzung des Schirms durch einen an einem Gitter gebeugten Elektronenstrahl (Abb. rechts) ist eine Häufigkeitsverteilung (je dunkler, desto häufiger wurde eine kleine Teilfläche getroffen). Es mag so klingen, als ob die QM hier unzureichend wäre, weil sie keine konkreten Aussagen bei Einzelbetrachtungen machen kann. Genau das Gegenteil trifft aber zu, denn die quantenmechanische Aussage entspricht der experimentellen Beobachtung. Man kann tatsächlich nicht exakt vorhersagen, an welcher Stelle des Schirms ein schwarzer Punkt entstehen wird, lediglich, dass bei sehr vielen Elektronen die erwähnte Häufigkeitsverteilung entsteht. Die statistische quantenmechanische Voraussage und der experimentelle Befund stimmen überein! Die Quantenmechanik kann keine Aussage über das genaue Verhalten von Einzelobjekten, sondern nur statistische Aussagen über eine Vielzahl von Teilchen machen! Ort und Impuls eines Teilchens sind nicht mehr gleichzeitig beliebig genau bestimmbar, sondern mit einer "naturgegebenen" Ungenauigkeit behaftet, die durch die Heisenbergsche Unschärferelation beschrieben wird.