Vergleich von elektrischer und schwacher Ladung

Elektroschwache Vereinigung - Vergleich von elektrischer und schwacher Ladung

Das Photon g und das Z⁰ ließen sich als Linearkombination der Zustände B⁰ und W⁰ darstellen. Bei der Darstellung fand man folgenden, zentralen Zusammenhang:

e = g ^. sinq_W

In Worten:
Die elektrische Ladung ist - bis auf eine Drehung um den Weinbergwinkel - so groß wie die schwache Ladung! Dies ist eine der wichtigsten Aussagen der elektroschwachen Vereinigung.

Der Weinbergwinkel kann experimentell auf mehrere Weisen bestimmt werden. Eine Möglichkeit ist die Bestimmung des Verhältnisses der Massen von W^+/- (m_W) zu der von Z⁰(m_Z):

m_W/m_Z = cosq_W

Als Durchschnittswert vieler verschiedener Messungen erhält man (üblicherweise wird der quadratische Sinuswert von q_W angegeben):

sin²(q_W) = 0,23124 +/- 0,00024 Damit ist sinq_W » 0,5.

Es gilt also e » 0,5^.g, d.h. e und g sind bis auf den Faktor 1/2 gleich groß. Wenn man die Kopplungsstärken der elektromagnetischen und schwachen Wechselwirkung also nur aufgrund der Ladung bzw. Kopplungskonstanten vergleicht, müsste die schwache Wechselwirkung etwa gleich stark sein wie die elektromagnetische. Dass in Wirklichkeit die elektromagnetische wesentlich stärker als die schwache Wechselwirkung ist, liegt am Propagatorterm der Austauschteilchen
(

). In den Nenner des Propagatorterms geht die Masse des

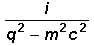Austauschteilchens quadratisch ein (siehe Propagatorterm rechts). Da die W- und Z-Bosonen eine sehr große Masse besitzen, das Photon hingegen masselos ist, ist der Propagatorterm der W- und Z-Bosonen wesentlich kleiner als der des Photons und bestimmt so die effektive Stärke der Wechselwirkung.

Erst der kleine Propagatoterm der W- und Z-Bosonen erklärt die "Schwäche" der schwachen Wechselwirkung im Vergleich zur elektromagnetischen Wechselwirkung.

Eine Folge des "Mischzustands Z⁰" ist, dass sich seine Kopplungsstärke von der der W-Bosonen unterscheidet. Die Kopplung der W-Bosonen ist unabhängig von der elektrischen Ladung der Fermionen an die sie koppeln (Universalität der schwachen Ladung g).

Die Kopplung des Z⁰ hängt davon ab! Dies führt zu einer Korrektur der schwachen Ladung g bezüglich des Z⁰zu einem g_Z, das von den Quantenzahlen Ladung Q und schwacher Isospin T₃ des Fermions abhängt.

Wir sind hier schon fast am Ende unserer Betrachtungen zur elektroschwachen Theorie. Auf der nächsten Seite werden wir noch besprechen, wie die schweren W- und Z-Bosonen zu ihrer Masse kommen.