|
Angeregte
Zustände & Co. - Diskrete Energieniveaus
von Atomen
 Was
versteht man unter einem Energieniveau?
Um
den Begriff Energieniveau eines gebundenen Systems zu klären,
betrachten wir am besten zuerst
ein Atom als Beispiel eines solchen Systems.
Atomen
kann Energie in Form von Strahlung oder über elastische
und inelastische Stöße zugeführt
werden. Zugeführte Energie wird von einem Atom kurz gespeichert und
dann in Form eines Photons (g-Quants)
abgegeben. Das Entscheidende dabei ist, dass Energie nicht kontinuierlich,
in
|
jeder beliebigen Menge, sondern nur in bestimmten Portionen
(sogenannten "Quanten") von Atomen
absorbiert und emittiert werden kann.
Dies
ist eine der wichtigsten Entdeckungen der Physik zu Beginn des 20. Jahrhunderts
und wurde zum ersten Mal in einem berühmten Versuch von den deutschen
Physikern James Franck und Gustav Ludwig Hertz (beide Nobelpreis
1925) gezeigt.
|
|
Der Franck-Hertz-Versuch
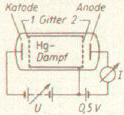
In einer mit Quecksilberdampf (Hg)
gefüllten Röhre werden Elektronen mit einer variablen Spannung U (kinetische Energie eU) zwischen Kathode und Gitter 1 beschleunigt (siehe Abb. rechts).
Anschließend durchfliegen sie den Quecksilberdampf (Gitter 1 bis 2). Zwischen Gitter 2 und der Anode liegt eine kleine Gegenspannung von 0,5 V an.
Elektronen, die unelastische Stöße mit Quecksilberatomen ausgeführt haben, können die Gegenspannung nicht überwinden.
Nur Elektronen mit einer Restenergie von mehr als 0,5 eV
treffen auf die Anode und tragen zum gemessenen Anodenstrom I bei. Man stellt fest, dass die Elektronen
nur dann kinetische Energie abgeben, wenn sie einen bestimmten Schwellenwert überschreitet (ca. 4,9 eV).
Franck und Hertz schlossen richtig daraus, dass
|
das Quecksilberatom erst
eine Energieportion von 4,9 eV absorbieren kann und keine kleinere.
Offensichtlich führten die Elektronen mit kleineren Energien nur elastische
Stöße aus und bei 4,9 eV plötzlich einen unelastischen
Stoß, bei dem sie ihre ganze kinetische Energie abgaben und nicht
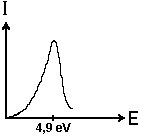
mehr weiterflogen. Die Abbildung rechts zeigt das zugehörige Energie-Stromstärke- Diagramm.
Die Stromstärke I, die die Elektronen verursachen, die ungestört
durch den Quecksilberdampf fliegen, bricht bei 4,9 eV ein.
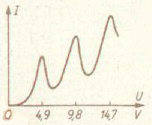
Erhöht man die Beschleunigungs- spannung U weiter, so erhalten die Elektronen soviel Energie, dass sie 2, 3 und mehr unelastische Stöße ausführen können.
Man erhält entsprechend in der Auswertung
bei ganzzahlig Vielfachen von 4,9 V auch Einbrüche des Anodenstroms I (siehe Graphik rechts unten)
|
|
 Erklärung:
Dem
Energiewert von
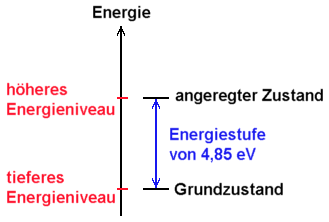
4,9 eV (genauer: 4,85 eV) entspricht im Atom eine sogenannte Energiestufe
zwischen
zwei Energieniveaus.
Das
Quecksilberatom befindet sich normalerweise im (Energie-) Grundzustand,
der durch die Zuführung der Energie 4,9 eV in einen angeregten
Zustand übergeht.
Das
Energieniveau des angeregten Zustands liegt also 4,9 eV über
dem Niveau des Grundzustands.
|
|
|
Unter
einem angeregten Zustand versteht man jeden Zustand, der gegenüber
dem Grundzustand mehr Energie besitzt (die ihm durch
|
"Anregung" zugeführt
wurde).
Den
Übergang von einem Energieniveau zum anderen bezeichnet man als Quantensprung.
|
|
Ein
Quantensprung findet aber nicht nur bei der Aufnahme von Energieportionen
statt sondern auch bei der Abgabe. Das angeregte Quecksilberatom wird nämlich
sehr schnell wieder in den Grundzustand übergehen, indem es ein g-Quant
emittiert, das die Energieportion von 4,9 eV wieder wegtransportiert.
Die Energie eines g-Quants
hängt über die Beziehung E = hn
= hc/l
mit seiner
Frequenz n
bzw. Wellenlänge
l
zusammen (h
Plancksches Wirkungsquantum, h = 6,602.10-34
Js). Um die 4,9 eV abzugeben, wird ein g-Quant
der Wellenlänge l
= hc/E = 253 nm (UV-Bereich) emittiert.
Das
Quecksilberatom - und mit ihm alle anderen Atome - besitzt nicht
nur
|
diesen einen angeregten Zustand, sondern sehr viele höhere
Energieniveaus. Jedem Übergang eines Atoms von einem Energieniveau
zum anderen entspricht die Absorption oder Emission einer bestimmten Energieportion
bzw. entsprechend für das g-Quant
eine charakteristische Wellenlänge. Man kann daher Atome (und auch
Moleküle) anhand der charakteristischen Wellenlängen der von
ihnen emittierten g-Quanten
identifizieren.
Die Gesamtheit der Wellenlängen aller Übergänge
zwischen Energieniveaus eines Atoms nennt man das charakteristische
Spektrum des Atoms.
|
|
Wenn
wir bisher vom angeregten Atom gesprochen haben, so muss man genauer eigentlich
von der Elektronenhülle des Atoms sprechen, denn der Kern spielt
dabei eine Nebenrolle (er verursacht das Coulomb-Potential in dem sich die Elektronen befinden). Die Anregung eines Atoms führt zu
einer Änderung des Zustands der Elektronenhülle. Dabei wird ein
Elektron aus einem energetisch tieferen Zustand in einen höheren gebracht.
Beim Zurück-"fallen" gibt es das besagte g-Quant
ab (siehe symbolischen Blitz 
in rechter Animation).
|
|
|
|
Nach
der Betrachtung und Untersuchung der diskreten Energiestufen stellt sich
folgende Frage: "Kann man diese Energiestufen erklären oder berechnen?".
Die Antwort lautet Ja und wurde von
|
der Quantenmechanik gegeben.
Die Quantenmechanik erlaubt es, z.B. die diskreten Energiestufen eines
Wasserstoffatoms zu berechnen.
|
|
Bevor wir auf der nächsten Seite zu Atomkernen und
weiteren Teilchen kommen, folgen noch zwei kurze Fragen:
|
