|
Angeregte
Zustände & Co. - Atomkerne und andere
Teilchen
|
Nach
der Erkenntnis, dass Atome diskrete Energiestufen besitzen, war es nicht
mehr weit zu dem Schritt, dieses Modell auf andere gebundene Systeme des
mikroskopischen Bereichs wie z.B. Atomkerne zu übertragen. Auch
Atomkerne können angeregt werden und bestimmte, diskrete Energieniveaus
"besetzen". Im Unterschied zum Atom, bei dem ein Elektron Energie abgibt
oder aufnimmt, sind es im Kern die Protonen und Neutronen, die auf
diskrete
|
Energieniveaus gehoben werden können. Dabei sind die Energiestufen
zwischen einzelnen Energieniveaus im Atomkern (keV- bis MeV-Bereich!)
um ein Vielfaches größer als in der Elektronenhülle (eV-
bis keV-Bereich). Dementsprechend sind die g-Quanten,
die vom Kern emittiert werden (z.B. "harte" g-Strahlung  ),
auch um ein Vielfaches energiereicher, als die der Hülle (z.B. sichtbares
Licht ),
auch um ein Vielfaches energiereicher, als die der Hülle (z.B. sichtbares
Licht ). ).
|
|
|
Es gibt aber noch mehr Systeme, die diskrete Energiestufen
besitzen. So haben die Teilchenphysiker festgestellt, dass auch gebundene
Systeme aus Elementarteilchen, wie Baryonen,
Mesonen,
das Positronium oder auch die
|
Quarkonium-Teilchen angeregte
Zustände besitzen. Auch diese Energiestufen verraten sich wieder durch
emittierte g-Quanten mit charakteristischen Energien.
mit charakteristischen Energien.
|
|
 Wovon
hängen die angeregten Zustände gebundener Systeme ab? Wovon
hängen die angeregten Zustände gebundener Systeme ab?
Die
verschiedenen Anregungszustände eines gebundenen Systems werden durch
Quantenzahlen  beschrieben.
beschrieben.
Um
dies anschaulich - aber nicht unbedingt streng physikalisch - zu verdeutlichen,
benutzen wir ein Modell.
Stellen wir uns ein Elektron vor. Es kreist im Abstand r um ein Zentrum, das es
aufgrund irgendeiner Wechselwirkung an sich bindet. Welche Energie besitzt
das Elektron?
Dafür gibt es verschiedene Möglichkeiten. Es besitzt sicher Rotationsenergie
aufgrund des Bahndrehimpulses, der in der Drehung im Abstand r um das Zentrum steckt.
Lassen wir es zusätzlich um seine eigene Achse rotieren, besitzt es
aufgrund dieses Spins (Eigendrehimpuls) noch mehr Energie.
Bahndrehimpuls
und Spin führen folglich
|
zu einer
bestimmten Gesamtenergie des Systems "Zentrum - Elektron". Wie wir aber bei
der Betrachtung des Spins und weiterer Quantenzahlen gesehen haben,
kann ein mikroskopisches Teilchen wie unser Elektron nur bestimmte "Portionen"
an Spin, Bahndrehimpuls etc. aufnehmen, die ein Vielfaches einer kleinsten
Einheit sind. Für die Angabe des Spins, des Bahndrehimpulses etc. hat
uns deshalb auch die Angabe einer Quantenzahl genügt, die angab,
wie oft die kleinste Einheit des Spins, des Bahndrehimpulses etc. in der Kugel
enthalten ist. Da ein quantisierter Spin
und ein quantisierter Bahndrehimpuls zu einer quantisierten Gesamtenergie
führen, genügt die Angabe der Quantenzahlen
zur Beschreibung der Gesamtenergie.
|
|
 Ein Teilchen mit Spin s = 0 und Bahndrehimpuls l = 1 wird sicher weniger Energie besitzen
und damit ein
Ein Teilchen mit Spin s = 0 und Bahndrehimpuls l = 1 wird sicher weniger Energie besitzen
und damit ein
|
niedrigeres Energieniveau besetzen als ein Teilchen mit Spin
s = 1 und Bahndrehimpuls l = 3.
|
|
|
An
diesem Beispiel sollte deutlich werden, dass man alle Energieniveaus eines
gebundenen Systems durch die Angabe von Quantenzahlen beschreiben
kann. Dabei führt eine Vielzahl von Quantenzahlen natürlich zu
einer Vielzahl
von Energieniveaus. Physiker verwenden zur Bezeichnung eines
bestimmten Zustands eine besondere Schreibweise. Es sei hier nur
|
erwähnt, dass es neben dieser Schreibweise auch noch eine Reihe von
Regeln gibt, nach denen Quantenzahlen kombiniert werden dürfen
und Regeln, die genau vorschreiben, ob ein Zustand überhaupt in einen
bestimmten anderen Zustand durch Anregung oder Emission übergehen
darf (sogenannte
Auswahlregeln).
|
|
Zum
Abschluss dieser Seite soll das Beispiel rechts zeigen, wie man die Energieniveaus
mit Quantenzahlen und der besonderen Schreibweise in einem sogenannten
Termschema
darstellt (Bsp.: Kalium). Am rechten Rand erkennt man die Energie-Achse.
Sie ist so skaliert, dass sie nicht die Gesamtenergie eines Zustands angibt,
sondern die Energie, die man braucht, um vom jeweiligen Zustand in den
höchstmöglichen zu kommen. Dementsprechend ist der unterste,
mit K gekennzeichnete Zustand der Grundzustand. Bei ihm bräuchte
man "einige keV", um ihn in den höchstmöglichen Zustand zu überführen.
Über
dem Diagramm erkennt man die von den Physikern verwendete Schreibweise
(z.B. "2P3/2").
Die "2", das "P" und
der Bruch "3/2" stehen
dabei jeweils für Quantenzahlen wie Spin,
|
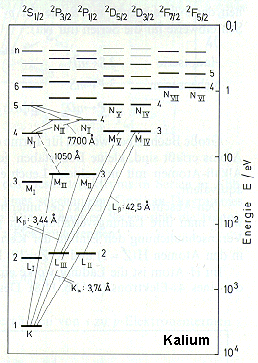 Drehimpuls etc.. Alle Querstriche
unter "2P3/2"
symbolisieren mögliche Zustände,
die alle zu "2P3/2"
gehören, sich aber durch eine weitere Quantenzahl (n, am linken Rand:
1, 2, 3, ...) unterscheiden.
Drehimpuls etc.. Alle Querstriche
unter "2P3/2"
symbolisieren mögliche Zustände,
die alle zu "2P3/2"
gehören, sich aber durch eine weitere Quantenzahl (n, am linken Rand:
1, 2, 3, ...) unterscheiden.
Schräge
Linien, die zwei Zustände verbinden, sind erlaubte Quantensprünge,
bei deren Übergang (von oben nach unten) ein
g-Quant
emittiert wird, das die daneben angegebene Wellenlänge in Angström
(1 Å = 10-10 m = 0,1 nm) besitzt.
(siehe
auch ![zum Literaturverzeichnis; [HAK 1993, S.180]](../button_gifs/booksm.gif) ). ).
|
|