Quantenzahlen - Eine Übersicht

Die Teilchen des Standard-Modells - Quantenzahlen

Einer der wichtigsten Unterschiede zwischen physikalischen Betrachtungen im makroskopischen Bereich der klassischen Physik und denen im mikroskopischen Bereich der Teilchenphysik ist, dass bestimmte Eigenschaften, die Teilchen besitzen, nur noch quantisiert, das heißt "in Portionen" angenommen werden können.
Z.B. kann ein Teilchen nur den Spin (Eigendrehimpuls) besitzen, der ein ganzzahlig Vielfaches der kleinsten

Einheit, h/2 ist. Es genügt folglich, für den Spin die Zahl anzugeben, mit der die kleinste "Portion" multipliziert wird. Solche Zahlen nennt man Quantenzahlen. Neben den Quantenzahlen, die mit bekannten Größen verbunden sind, wie eben z.B. der Spin oder auch die elektrische Ladung, gibt man zur Unterscheidung von Teilchen und ihrer Zustände noch eine Reihe weiterer Quantenzahlen an.

Die Quantenzahl eines zusammengesetzten Teilchens ist die Summe der Quantenzahlen seiner Bausteine

Folgende Übersicht soll die wichtigsten Quantenzahlen, der Teilchenphysik vorstellen:

Ladung Q	Spin s	z-Komponente des Spins S_z
Bahndrehimpuls l bzw. L	Gesamtspin j bzw. J	Baryonenzahl B
Isospin I	z-Komponente des Isospins I₃	Hyperladung Y
Charm c	Strangeness S	Leptonenzahl L

1. Die elektrische Ladung Q à die Ladungs-Quantenzahl Q

Auch die elektrische Ladung ist quantisiert. Sie kann nur als Vielfaches der Elementarladung e (bzw. 1/3 e) vorkommen.

Quarks tragen die elektrische Ladung -1/3 e oder +2/3 e. Ihnen wird daher, je nach Flavour, die Ladungsquantenzahl Q = -1/3 oder Q = +2/3 zugeordnet.
Das Proton trägt eine positive Elementarladung, es hat deshalb Q = +1
Das Elektron trägt eine negative Elementarladung, es hat Q = -1

2. Die Spin-Quantenzahl s

Mikroskopische Teilchen können nur Eigendrehimpulse (Spins) annehmen, die ein ganzzahlig Vielfaches von h/2 = h/4p (h Plancksches Wirkungsquantum) sind. Zur Angabe des Spins eines Teilchens

genügt es folglich die Zahl anzugeben (die sogenannte Spin-Quantenzahl s), mit der h multipliziert werden muss, um den Spin zu erhalten.

Quarks und Elektronen besitzen den Spin h/2. Man ordnet ihnen die Spin-Quantenzahl s = 1/2 zu.

Siehe hierzu auch

3. Die z-Komponente des Spins S_z

Die Spin-Quantenzahl - kurz Spin genannt - eines Teilchens drückt den Eigendrehimpuls aus. Damit ist aber noch nicht festgelegt, in welche Richtung sich ein Teilchen dreht, ob rechts-

oder

linksherum.
Um einen Drehsinn anzugeben, muss man eine Achse festsetzen, bezüglich der man von rechts- oder linksherum sprechen kann. Man nimmt dazu die Achse, bezüglich der das Teilchen den maximalen Spin besitzt. Die Physiker legen üblicherweise immer die z-Achse in diese Richtung. Der Drehsinn wird durch das Vorzeichen unterschieden. Rechtsherum zählt positiv, linksherum negativ. Die zugehörige Quantenzahl,

die das Vorzeichen berücksichtigt, heißt z-Komponente des Spins S_z. Elektronen können je nach Drehsinn S_z = 1/2 oder S_z = -1/2 haben. Diese Unterscheidung nennt man auch "Spin up (á)" oder "Spin down (â)", was aber nichts mit den Quarkflavours up und down zu tun hat. Ein up-Quark kann z.B. "Spin up oder down" haben!
Die Drehsinnberücksichtigung hat aber auch zur Folge, dass sich bei zusammengesetzten Teilchen die einzelnen Spins nicht nur zu einem größeren Spin addieren, sondern auch gegenseitig aufheben können.

Das p-Meson besitzt z.B. den Spin 0, weil sich die Spins der enthaltenen Quarks und Antiquarks gegenseitig aufheben (einmal S_z = 1/2 und einmal S_z = -1/2).

Baryonen aus drei Quarks können dagegen maximal Spin 3/2 haben, wenn die drei einzelnen Spins der enthaltenen Quarks alle S_z = 1/2 betragen. Ist einer davon andersherum gerichtet, so ist S_z des Baryons nur noch 1/2 + 1/2 + (-1/2) = 1/2.
Wenn man alle möglichen Kombinationen durchspielt, erhält man als mögliche z-Komponenten des Spins für Baryonen: -3/2, -1/2, 1/2 und 3/2.
Daraus kann man auch sofort die allgemeine Regel ableiten, dass zusammengesetzte Teilchen mit (Gesamt-) Spin s die z-Komponenten -s, -s+1, -s+2, ..., s-2, s-1 oder s haben können.

Ein zusammengesetztes Teilchen mit s = 1 kann für S_z die Werte -1, 0 und 1 annehmen.

Baryonen, deren Quarks zusätzlich zum Spin einen Bahndrehimpuls besitzen, nennt man "Baryonische Resonanzen".

Siehe hierzu auch

4. Die Bahndrehimpulsquantenzahl l bzw. L

Teilchen besitzen neben Spins (Eigendrehimpulse) auch einen Drehimpuls bezüglich der Rotation um einen Punkt (z.B. "P" in Abb. rechts) außerhalb einer Achse durch ihren Schwerpunkt (Bewegung auf einer "Bahn" mit der Bahngeschwindigkeit v). Diesen Drehimpuls nennt man Bahndrehimpuls. Der Bahndrehimpuls ist quantisiert. Er kann für Teilchen des mikroskopischen Bereichs nur ganzzahlig Vielfache von h betragen. Wie andere quantisierte Größen wird der Bahndrehimpuls auch durch eine

Quantenzahl, die Bahndrehimpulsquantenzahl l (für ein einzelnes Teilchen) oder L (für mehrere Teilchen) angegeben. Teilchen können l = 0, 1, 2, 3, ... besitzen. Historisch bedingt benutzen die Physiker dafür aber noch eine andere Schreibweise. Sie bezeichnen den Zustand eines Teilchens mit l = 0 mit "S", l = 1 mit "P", l = 2 mit "D" etc.. Z.B. besitzt ein P-Zustand immer den Bahndrehimpuls 1. Alle verwendeten Buchstaben in der Übersicht:

Drehung um Punkt P mit Bahngeschwindigkeit v

Quantenzahl l = ...	0	1	2	3	4	5 ...
verwendeter Buchstabe	S	P	D	F	G	H ...(alphabetisch weiter)

Siehe hierzu auch

5. Gesamtspin j bzw. J

Neben dem Spin s (Eigendrehimpuls) eines Teilchens bzw. dem zusammengesetzten Spin S eines Teilchensystems (z.B. Baryon), besitzt ein Teilchen noch einen Bahndrehimpuls l. Spin und Bahndrehimpuls werden nach bestimmten Regeln zu einem

Gesamtdrehimpuls bzw. Gesamtspin J addiert. Wenn klar ist, dass die Regeln beachtet werden müssen, schreibt man oft einfach J = L + S oder für einzelne Teilchen j = l + s (kleine Buchstaben) wobei es sich streng genommen um eine Vektoraddition handelt!.

Siehe hierzu auch

6. Die Leptonenzahl L

Bei Experimenten hat sich herausgestellt, dass die Anzahl der Leptonen vor und nach einer Reaktion erhalten bleibt. Leptonen werden nicht beliebig erzeugt oder vernichtet, außer es kommt zur Paarvernichtung (Annihilation) oder -erzeugung zwischen Teilchen und Antiteilchen. Man ordnet daher Teilchen die sogenannte Leptonenzahl L zu und kann damit rechnerisch überprüfen ob die Summe der Leptonenzahlen erhalten bleibt.
Ein Lepton erhält L = +1, Antileptonen L = -1 und alle anderen Elementarteilchen L = 0. Bei den Leptonen unterscheidet man noch einmal zwischen den verschiedenen Generationen. So

ordnet man der entsprechenden Generation eine e^--, eine m^-- und eine t^-- Leptonenzahl (L_e, L_m und L_t) zu, die einzeln erhalten bleibt.
Beispiel (Zerfall des Müons):
m^- à n_m+ e^- + n_e
dabei gilt für die Leptonenzahlen:
L_m(m^-) = +1 und L_m(n_m) = +1; L_e(e^-) = +1; L_e(n_e) = -1
Man erkennt, dass "die Summe aller" L_m und L_e sowohl vor als auch nach dem Zerfall gleich ist.

7. Die Baryonenzahl B

Die Baryonenzahl B ist analog zur Leptonenzahl die Quantenzahl, die ausdrückt, ob ein Teilchen Baryon, Antibaryon oder etwas anderes ist. Ein Baryon erhält die Baryonenzahl B = 1,

ein Antibaryon B = -1.
Da ein Baryon aus drei Quarks besteht, erhält ein Quark B = 1/3 und ein Antiquark B = -1/3. Alle anderen Elementarteilchen haben B = 0.

8. Der Isospin I

Da die starke Kraft, die die Nukleonen zusammenhält, unabhängig von ihrer elektrischen Ladung ist, wurde schon vor der Entdeckung der Quarks vermutet, dass Proton und Neutron sehr eng verwandte Teilchen sein müssen. Sie wurden daher als zwei verschieden Zustände - der eine elektrisch geladen, der andere neutral - ein und desselben Teilchens, des Nukleons, betrachtet. Neben diesem Beispiel findet man noch eine Reihe weiterer Teilchen, für die die starke Kraft ähnlich ist und daher nur als "verschiedene Zustände eines Teilchens" betrachtet werden, so z.B. das p⁺, p⁰ und p^--Meson. Zu ihrer Unterscheidung führt man einen abstrakten "Spin", den Isospin I ein, der außer dem Namen aber nichts mit dem richtigen Spin zu tun hat und für den es auch keine anschauliche Vorstellung wie den Eigendrehimpuls o.ä. gibt. Man ordnet einem Teilchen, das in verschiedenen Zuständen vorkommt, einen "Isospin I"

zu, der angibt, wie viele verschiedene Zustände des einen Teilchen vorkommen. Die eigentliche Unterscheidung erfolgt wie beim Spin durch die z-Komponente. Der Isospin I gibt den Maximalwert vor und die Komponente in z-Richtung (beim Isospin mit I₃ bezeichnet, weil die z-Achse meist die 3. der drei Raumrichtungen ist) liefert die eigentliche Unterscheidung der Teilchen durch unterschiedliche Vorzeichen bzw. Werte. Die Gruppe aus den Teilchen, die nur verschiedene Zustände eines Teilchens darstellen, nennt man allgemein Multiplett. Zwei Teilchen wie z.B. Proton und Neutron bilden ein Dublett (n = 2), drei Teilchen wie z.B. beim p⁺, p⁰ und p^--Meson ein Triplett (n = 3) usw..
Der Maximalwert des Isospins berechnet sich nach der Formel:
I = n/2 - 1/2

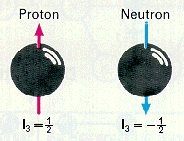
Für ein Dublett (n = 2), wie das aus Proton und Neutron, erhält man:
I = (2 : 2) - 1/2 = 1/2. Die Nukleonen haben also Isospin I = 1/2
Für ein Triplett, wie das der p-Mesonen, erhält man:
I = (3 : 2) - 1/2 = 1. Die Pionen haben also Isospin I = 1
Ein Quartett hat Isospin I = 3/2, ein Quintett I = 2 usw.
Der Isospin betrifft nur die starke Wechselwirkung und somit auch nur die Quarks bzw. Hadronen. Wenn es denn nötig ist, so könnte man Leptonen den Isospin Null zuordnen.

9. Die z-Komponente des Isospins I₃

Die z-Komponente des Isospins I₃unterscheidet die Teilchen eines Isospin-Multipletts (z.B. die des Nukleonen-Dubletts) durch verschiedene Werte. In Anlehnung an den Spin erfolgt auch hier die gleiche Unterscheidung:

Für I = 1/2 gibt es die z-Komponenten I₃= 1/2 und I₃= -1/2
Für I = 1    gibt es die z-Komponenten I₃= -1, I₃= 0, und I₃= +1
Für I = 3/2 gibt es I₃= -3/2, -1/2, 1/2 und 3/2 usw.
Das Proton hat I₃= 1/2, das Neutron hat I₃= -1/2
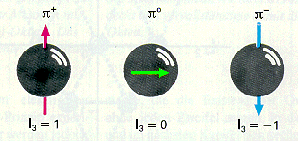das Pionen Isospin-Triplett Das p⁺-Meson hat I₃= +1, das p⁰-Meson hat I₃= 0 und das p^--Meson hat I₃= -1
Allgemein gilt, dass man dem Teilchen eines Multipletts, das die größte positive Ladung trägt, den größten I₃-Wert, also I₃ = I zuordnet und dann die restlichen I₃-Werte mit absteigender Ladung der Größe nach verteilt.

Man erkennt an den Beispielen einen Zusammenhang zwischen der elektrischen Ladung und der z-Komponente des Isospins. Diesen Zusammenhang drückt eine weitere Quantenzahl aus, die Hyperladung Y.

10. Die Hyperladung Y

Die Quantenzahl "Hyperladung" verbindet die elektrische Ladung und den Isospin. Sie berechnet sich einfach aus Q und I₃:
Y = 2^.(Q - I₃)
Das Proton hat z.B. die Hyperladung Y = 2^.(1 - 1/2) = 1
Das Neutron hat die Hyperladung Y = 2^.(0 - (-1/2)) = 1. Beide besitzen also die gleiche Hyperladung!

11. Die Charm-Quantenzahl c

Die Charm-Quantenzahl c gibt an, ob ein Elementarteilchen ein charm-Quark, charm-Antiquark oder keines von beiden ist. Dabei erhält ein charm-Quark die Quantenzahl c = 1, ein charm-Antiquark

c = -1 und alle anderen Elementarteilchen c = 0. Zusammengesetzte Teilchen haben als Charm-Quantenzahl wieder die Summe der c`s ihrer Bausteine.

Das J/Y-Meson (Charmonium) aus einem c-Quark und einem c-Antiquark hat c = +1 + (-1) = 0.

12. Die "Seltsamkeit" oder "Strangeness" à die Strangeness-Quantenzahl S (kurz: Strangeness)

Ursprünglich wurden mit dieser Quantenzahl Teilchen gekennzeichnet, die sich seltsam (engl. strange) verhielten, was ihre Erzeugungszeit und Lebensdauer betraf. Heute wissen wir,

dass S einfach der Unterscheidung von strange-Quark und strange-Antiquark dient. Ein strange-Quark hat S = -1 und ein strange-Antiquark S = +1. Alle anderen Elementarteilchen haben S = 0.

Das W^--Baryon aus drei strange-Quarks hat z.B. die Strangeness S = -3

Das Antiteilchen des W^--Baryons aus drei strange-Antiquarks hat dann die Strangeness S = +3