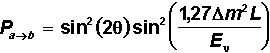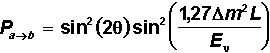|
Leptonen
im Standard-Modell - Wahrscheinlichkeit für
Flavour-Änderungen
|
Im
Standardmodell haben alle Neutrinos die Masse null. Dies ist aber nicht
zwingend notwendig, es ist lediglich die einfachste Annahme. Auch Neutrinomassen
ungleich null können im Rahmen des Standardmodells untergebracht werden,
wobei es verschiedene Möglichkeiten gibt. Falls die Neutrinomassen
ungleich null sind, besteht die Möglichkeit, dass sich (auch im Vakuum)
eine Neutrinosorte in die
|
andere umwandelt und umgekehrt (z.B.
ne
à
nm
à
ne).
Dies geschieht mit einer bestimmten Umwandlungsrate, ausgedrückt durch
den Mischungswinkel q.
Man bezeichnet die Umwandlungen als Neutrino-Oszillationen. Aus der Beobachtung
von Neutrino-Oszillationen könnte man folglich zwingend schließen,
dass die Neutrinos massebehaftet sein müssen.
|
|
|
Sollte es Neutrino-Oszillationen geben (gleichbedeutend
sind Anti-Neutrino-Oszillationen), so wäre die Wahrscheinlichkeit
dafür, dass sich
|
ein Neutrino mit Flavour a im Abstand L von
der Quelle in ein Neutrino mit Flavour b (z.B.
nm
à
nt)
verwandelt Paàb:
|
|
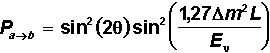
Die
Wahrscheinlichkeit Paàb
für eine
Flavouränderung hängt ab ...
... von der Differenz der Massenquadrate der beiden Neutrinos Dm2
= |ma2 - mb2|
... von der
Energie des Neutrinos En
... vom Abstand
L von der Neutrino-Quelle bzw. dem Entstehungsort der Neutrinos
... vom Neutrino-Mischungswinkel q
(vgl. Cabibbo-Winkel) 
| Der
Faktor 1,27 ist so gewählt, dass die Teilchenphysiker ihre
gewohnten Einheiten "GeV" für die Energie,
|
"km" für die Länge
und "(eV)2" für
das Quadrat einer Masse verwenden können.
|
|
So
weit, so gut, aber wo soll man nun nach welchen Neutrinos suchen, wenn
man nicht weiß, wie lange die Strecke ist, nach der sie ihren Flavour
ändern?
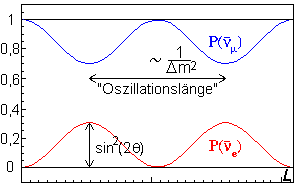
Entscheidend
ist, dass der Abstand zwischen zwei Minima in der Wahrscheinlichkeit (nennen
wir ihn "Oszillationslänge") proportional zu 1/Dm2
ist.
Als Beispiel sei das KARMEN-Experiment, bei dem u.a. ein Myon-Antineutrinostrahl
untersucht wird, angeführt. Die rechte Abbildung zeigt die Wahrscheinlichkeiten
dafür, dass sich in diesem Strahl durch Oszillation ein Elektron-Antineutrino
befindet (P(ne), rote Kurve).
Die blaue Kurve gibt an, wie sich zwangsläufig die Wahrscheinlichkeit
für die Müon-Antineutrinos verändert (P(nm)).
|
|
Es gilt P(ne)
+ P(nm)
= 1. Man erkennt, dass es Bereiche gibt, in denen die Wahrscheinlichkeit,
ein ne
zu finden,
maximal wird. Der Maximalwert ist sin2(2q),
hier etwa 0,3.
|
|
 Eine
alltägliche Erfahrung ist, dass die Differenz zweier Massen
in etwa die gleiche Größenordnung besitzt wie ihre absoluten
Massen. So liegt z.B. die Differenz der Massen zweier Menschen im Durchschnitt
sicher nicht im "mg"-Bereich, sondern beträgt meist einige "kg",
liegt also in der gleichen Größenordung wie die absolute Masse
von durchschnittlich ca. 70 kg. Es
|
liegt nahe, auch aus der Differenz
der Massenquadrate zweier Neutrinosorten auf die Größenordnung
ihrer absoluten Masse zu schließen. Dieser Rückschluss kann
aber nicht gezogen werden, da z.B. die Massen der Neutrinos extrem unterschiedlich
sein könnten, man denke dabei nur an die Massenverhältnisse bei
Leptonen (Verhältnisse bis zu 1:4000!). |
|
|
Die
Proportionalität der Oszillationslänge zu 1/Dm2
hat daher zur Folge, dass "je kleiner die
Differenz
|
der Massenquadrate der Neutrinos ist, desto größer
muss die Oszillationslänge sein".
|
|
|
Das Prinzip jeder Suche nach Neutrino-Oszillationen
ist es daher, theoretisch zu bestimmen, wie viele Neutrinos mit Flavour
a an einer Stelle erzeugt werden (künstlich oder natürlich, z.B.
in der Atmosphäre) und zu zählen, wie viele dieser Neutrinos
im Abstand L
|
von dieser Quelle noch vorhanden sind. Detektoren zählen
die Neutrinos über Teilchenreaktionen, die für ihren Flavour
charakteristisch sind. Sind die beiden Zahlen unterschiedlich, so müssen
Neutrinos während des Fluges (über die Länge L) ihren
Flavour geändert haben.
|
|
|
Es gab und gibt eine Vielzahl von Experimenten mit unterschiedlich
langen Messstrecken, angefangen bei wenigen Metern über Strecken
in der Größenordnung bis 1 km. Eine Reihe von Experimenten
bis zu einer Länge von 730 km sind bereits geplant und genehmigt.
Als Neutrino-Quellen dienen Reaktoren und Beschleuniger, in denen
|
Neutrinos
bei Teilchenreaktionen erzeugt werden. All diese Experimente konnten allerdings
bisher keine fehlenden Neutrinos nachweisen. Allerdings konnten mit ihnen
Obergrenzen für 1/Dm2
bestimmt werden. Für neue Messungen müssen wesentlich längere
Messstrecken gewählt werden.
|
|
|
Die längste auf der Erde realisierbare Neutrino-Flugstrecke
ist der Erddurchmesser. Eine entsprechende Messapparatur, der Super-Kamiokande,
wurde in Japan
|
errichtet und lieferte nach eineinhalbjähriger Messung
Mitte 1998 ein erstaunliches Ergebnis. Mehr dazu auf der nächsten
Seite.
|
|
|
