4 Az erős kölcsönhatás $\alpha_s$ csatolásának meghatározása

4.1 Az erős kölcsönhatás $\alpha_s$ csatolása

A négy alapvető kölcsönhatás mindegyikét egy csatolással jellemezhetjük, amely az erősségét meghatározza. A leggyengébb a gravitációs erő a G csatolással. Az elektromágneses kölcsönhatás csatolását $\alpha$-val jelöljük, az erős kölcsönhatásét pedig $\alpha_s$-sel. Ezek a csatolások, amelyek meghatározzák a különböző kölcsönhatások és folyamatok erősségét, a természet legalapvetőbb fizikai paraméterei közül valók.

4.2 A 2 jetes események

Az $e^+e^-$ megsemmisülése során, ha az ütközés magas energiája hadronná alakul az többnyire két ellentétes irányú részecskezáport hoz létre. Ez a Z részecske keletkezésével kapcsolatos, amely később egy kvarkra és egy antikvarkra bomlik. Ezek a kvarkok nagy sebességgel távolodnak egymástól, de 1 fm (1 fm = $10^{-15}$ m) körüli távolság felett az erős kölcsönhatás megakadályozza, hogy az egyes kvarkok távolabbra kerüljenek egymástól. Ehelyett újabb kvark és antikvark párok keletkeznek. Ez a folyamat végül egy részecskezáport hoz létre, mely főként az eredeti kvarkkal és antikvarkkal megegyező irányban mozgó mezonokból áll. (A mezon olyan részecske, amely egy kvarkból és egy anti-kvarkból áll.) Ezeket a részecskezáporokat nevezzük elfogadott rövid angol nevükön jeteknek (ejtsd: dzset).

Egy ábra egy két-jetes eseményről

4.3 A 3 jetes események

Néha egy nagy energiájú gluont bocsájt ki az egyik kvark. Ekkor ez a gluon is részecskezáport, azaz jetet hoz létre. Ez vezet a tiszta 3 jetes eseményhez.

A három jetes esemény mutatja, hogy létezik gluon

4.4 A 4 jetes események

Akár mind a két kvark kibocsájthat egy nagyenergiájú gluont, ekkor 4 jetes esemény jön létre. Annak a valószínűsége, hogy ez történik nagyon kicsi az előbbiekhez képest.

A több jetes esemény a gluon és az erős köcsönhatás létezésének bizonyítéka. Ezeknek az eseményeknek az aránya közvetlenül függ az erős kölcsönhatás $\alpha_s$ csatolásától.

Határozzuk meg a kvark eseményekben a jetek számát! Számoljuk meg mennyi:

• két jetes,
• három jetes,
• négy vagy több jetes esemény van!

Az eseménynézőben a színek alapján különíthetőek el az egyes jetek.

Ugrás az eseménynézőre

Határozzuk meg a a több jetes események arányát! Határozzuk meg a három jetes és két jetes események hánydosát, hogy megkaphassuk az erős kölcsönhatás csatolását - az erős kölcsönhatás leírásának egyik legfontosabb paraméterét!

A 91 GeV energiájú $e^+e^-$ ütközések nagyjából 70%-ában kettő vagy több jet jön létre. A két jetes események a két kvarkra (kvarkra és antikvarkra) vezethetőek vissza; a három jetes események pedig a két kvarkra és egy gluonra, ahol az egyik kvark bocsájtotta ki a gluont. A gluon kibocsájtás erős kölcsönhatásban történik, emiatt a gluon keletkezése arányos az erős kölcsönhatás csatolásával, $\alpha_s$-sel. Tehát, ha megszámoljuk a két és három jetes események számát, akkor a következőképp határozhatjuk meg $\alpha_s$-et:

$$\alpha_s=k N_{\mbox{3 jet}}/ N_{\mbox{2 jet}}$$

A részecskejetek száma függ a jetkereső programtól és attól a felbontási paramétertől is, amely meghatározza, hogy milyen közeli részecskenyomokat soroljunk azonos jetbe.

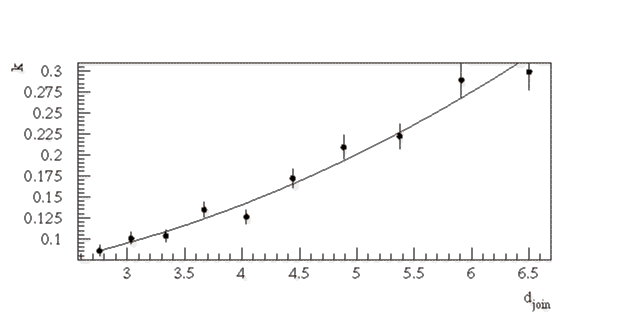
A két és három jetes események száma függ a jetkereső program felbontási paraméterétől ($d$), amely azt jelenti, hogy a $k$ konstansnak különböző értékei lesznek a $d$ különböző értékei esetén. A $k$ függése a $d$-től a következő ábrán látható.

Az eseménynézőben a felbontási paraméter értéke $d$=5 GeV/c. A kísérlet végrehajtásához meg kell számolni a három-jetes és két-jetes események számát, meghatározni a hányadosukat, leolvasni a $k$ konstans értékét, majd ezekből kiszámolni az erős kölcsönhatás csatolását. Az $\alpha_s$ RELATÍV hibája kiszámolható a következőképpen.

$$\frac{\Delta\alpha_s}{\alpha_s} = 0,1+ \frac 1{\sqrt{N_{\mbox{3-jet}}}} + \frac 1{\sqrt{N_{\mbox{2-jet}}}}$$

ahol 0,1 a $k$ hibájának járuléka, a másik két tag pedig a 3-jetes és 2-jetes események hibájának járuléka.

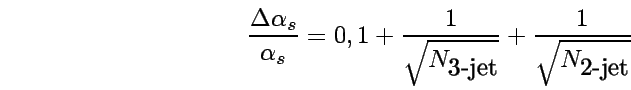
További olvasmányok:
[1]Ann. Rev. Nucl. Sci. 31 (81) 231     [2] Phys. Rev. D40 (89) 1385
valamint
[3]Phys. Lett. 89B (79) 139     [4] Z.Phys. C6 (80) 235
[5]Phys. Lett. 91B (80) 142     [6] Phys. Lett. 94B (80) 437
[7]Phys. Lett. 97B (80) 459     [8] Phys. Lett. 108B (82) 63
[9]Phys. Lett. 110B (82) 329     [10] Phys. Lett. 119B (82) 239
[11]Phys. Rev. D28 (83) 228     [12] Phys. Rev. Lett. 50 (83) 2051
[13]Z.Phys. C26 (84) 157     [14] Z.Phys. C25 (84) 231
[15]Phys. Rev. D29 (84) 580     [16] Phys. Lett. 138B (84) 311
[17]Phys. Rev. D31 (85) 2724     [18] Phys. Rev. Lett. 54 (85) 1750
[19]Phys. Lett. 180B (86) 181     [20] Phys. Lett. 199B (87) 291
[21]Phys. Lett. B215 (88) 175     [22] Phys. Lett. B252 (90) 159