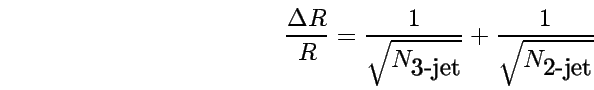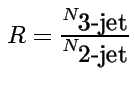 hányados
hányados
Ha kevés eseményt vizsgálunk, a statisztikai hiba elég nagy
lehet. A statisztikai hibák N megfigyelés esetén 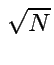 . A
relatív hiba:
. A
relatív hiba:

Abban az esetben, ha az összes események számát rögzítettnek vesszük, és csak két lehetséges kimenet lehetséges (lepton-esemény vagy kvark esemény), akkor a másféleképpen számoljuk a becsült hibát:
Ha összesen N számú esemény van,
az i típusú eseményből pedig ![]()
az i típusúak aránya 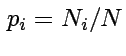 ,
,
akkor az ![]() hibája (standard deviációja)
hibája (standard deviációja)
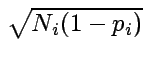 .
.
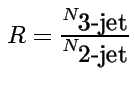 hányados
hányados
Mind az
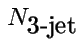 , mind az
, mind az
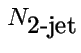 hibával
rendelkezik. Ezt a kettőt össze kell kombinálni. A hányados relatív
hibája:
hibával
rendelkezik. Ezt a kettőt össze kell kombinálni. A hányados relatív
hibája: