When pool balls (or particles) approach the speed of light, c, their properties are affected according to special relativity. (The Lorentz factor and other results from special relativity will be assumed as their derivation lies outside the focus of this website.)
Relative to a stationary observer, the moving particle (speed v) behaves as if its mass (m0) is greater, than when it is as rest, by the Lorentz factor:
|
(1) |
where
| |
(2) |
So momentum becomes:
|
|
(3a) |
|
|
(3b) |
The energy of the particle becomes:
|
|
(4) |
This energy E is called the total energy of the particle because it is made up of its rest energy, m0c2, and its kinetic energy. We can relate the total energy E directly to p by combining equations (3) and (4) to eliminate the particles velocity, to give
|
|
(5) |
Try this for yourself.
Derivation if you want to cheat!
Can you also show that, when beta becomes much less than 1, this reduces to the non-relativistic form:
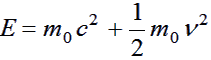 |
(6) |
Time also appears to go slow for the moving particles. A time interval Δt for the particle becomes lengthened to γΔt, as measured by the stationary observer. This is particularly important when measuring the lifetime of particles which are travelling at relativistic speeds - see section 4 'Lifetime'****link here???.