|
Calculating K0 Rest Mass
To calculate the rest mass of the K0
is not simple. We have to deduce its mass
from the measured properties of the pions. You determine the momentum of each pion by measuring the
radius of curvature of their tracks as you did for the particles in the
previous exercise. The equation (1) for the K0
rest mass (mK)
consists of terms relating solely to the pions. (Derivation)
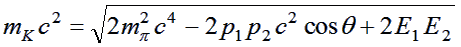 |
(1) |
 |
(units: GeV/c) |
(2) |
θ is the included angle between the direction of motion taken by each
pion, as shown below:
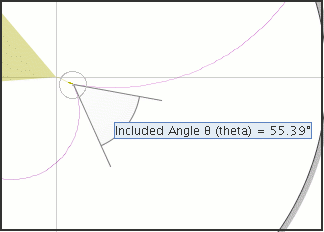
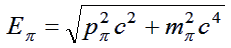 |
(3) |
Neutral kaon rest mass (mK) = 0.497
GeV/c2
Example
Kaon Mass Calculation
|
|
Calculating K0 Lifetime
The K0 mean lifetime is
the average time it exists from creation, when the incident electron and
positron annihilate, until decay when the K0
degenerates
into a π+, π-
pair. Particle decay is a random process that leads to an exponential
distribution of observed decay times. Instead of measuring these decay
times, which in reality are exceedingly small, we can measure the decay
lengths of the K0 - which are recorded by the detector.
This is the distance travelled by the K0
from creation,
at the origin where the electron-positron annihilation
takes place, to the decay point where the pions begin their trajectories -
called the 'vertex'.
Therefore, we can determine the K0
mean decay length (L) and then use this to calculate the
K0 mean decay time (τ),
for a particular beam energy.
You can estimate a value for L by measuring many
decay lengths (l), for the same
Incident beam energy, and calculating the mean. The decay time (τ)
is given by:
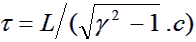
|
(1) |
where
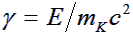 |
(2) |
where mK is the
K0 rest mass
which you determined in the first part of the exercise, c is the
speed of light and the value of E, you chose yourself. (Derivation
of formula and example calculation)
|
|
|
 > > 
|

