You have seen that each firing sequence can result in a different charged particle antiparticle pair being formed. The particles are colour coded; it is your task to identify them by determining their rest masses.
The relativistic equation connecting momentum, magnetic field and radius is:

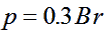(units: GeV/c)

(1)

Derivation
   
You should use this equation to determine the momentum of your particle by making measurements of the radius of curvature of its track.(explanation of radius calculation).

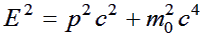(2)

where E is the total energy of the particle (kinetic plus rest energy) and m₀ is the rest mass. We can see that for a particle at rest (p = 0) this equation reduces to the familiar, E = m₀c².

Because energy is conserved, the total energy before annihilation equals the total energy after annihilation. In our case, before annihilation, the electron and positron each have an energy equal to the beam energy, therefore the total energy of the system is twice this amount. After annihilation, when a particle-antiparticle pair are formed, each particle takes half of the available energy: equal to the original beam energy. Therefore in equation (2), E = Incident beam energy.

We now know both the energy and momentum of each particle in the charged particle pair. Equation (2) can be rearranged to determine their rest masses:   

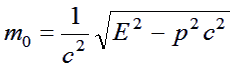(3)

The computer selects, at random, from four charged particle pairs, shown below with their rest masses:

Run the experiment several times until you have produced and identified all four particle antiparticle pairs.