Wellenlänge und Impuls von Teilchenstrahlen - Hohe Energien und große Massen Bisher haben wir den Wellencharakter der Teilchenstrahlen betont und ihn über die De-Broglie- Beziehung mit der Teilcheneigenschaft Impuls verbunden. Es gibt aber, neben dem Erreichen sehr kleiner Wellenlängen des Teilchenstrahls, noch einen zweiten wichtigen Aspekt, warum Teilchen in Beschleunigern extrem hohe Energien zugeführt werden: In vielen Stoßexperimenten sollen Teilchen großer Masse erzeugt werden. Da Masse und Energie proportional sind (E = mc2), mit dem Proportionalitätsfaktor c2, muss die Gesamtenergie E eines Stoßes, bei dem sehr schwere Stoßprodukte entstehen sollen, entsprechend hoch sein. Der Einfachheit halber geben die Teilchenphysiker die Masse eines Teilchens in der Einheit [m] = [E]/c2 = 1 eV/c2 an. Das Z0-Boson hat die relativ große Masse von m = 91,2 GeV/c2. Es konnte deshalb erst experimentell nachgewiesen werden, nachdem ein entsprechender Beschleuniger eine Schwerpunktsenergie von mehr als  91,2 GeV erreichen konnte (siehe Bsp. unten). Dies war zum ersten Mal 1983 in einem Proton-Antiproton-Speicherring (engl. collider) am CERN möglich. Speicherringe in Verbindung mit Kollisionsexperimenten haben den Vorteil, dass man mit ihnen leichter höhere Schwerpunktsenergien erreichen kann, als mit dem Beschuss von festen Targets.  Der Grund dafür ist, dass die Schwerpunktsenergie, die für die Erzeugung neuer Teilchen relevant ist, beim Beschuss eines festen Targets mit der Wurzel der Strahlenergie zunimmt. Möchte man z.B. die Schwerpunkts- energie eines solchen Experiments verdoppeln, so muss man die Strahlenergie vervierfachen.  Im Gegensatz dazu nimmt die Schwerpunktsenergie bei Kollisionsexperimenten an Speicherringen linear mit der Strahlenergie zu. Das heißt, dass zur Verdopplung der Schwerpunktsenergie die Strahlenergie "nur" verdoppelt werden muss. Beispiel: Zur Erzeugung der Vektorbosons Z0 musste mit der Kollision eines Protonen- mit einem Antiprotonen- Strahl eine Schwerpunktsenergie von etwa 91,2 GeV erreicht werden. Wir wollen uns kurz überlegen, wie hoch dazu die Strahlenergie sein muss. Dazu gehen wir davon aus, dass wir bereits wissen, dass das Z0 91,2 GeV/c2 schwer ist, was die Forscher bei dessen Endeckung natürlich noch nicht so genau wussten. Die Reaktion, die als Produkt ein Z0 enthalten soll, kommt durch die Wechselwirkung eines up-Quarks und eines up-Antiquarks zustande: (u + u à Z0 + g + (X) ) Das up-Quark ist Teil eines Protons (uud) und das up-Antiquark ist Teil eines Antiprotons (uud). Das bedeutet, dass sich die nötige Schwerpunktsenergie nicht auf Proton und Antiproton bezieht sondern auf die enthaltenen Quarks bzw. Antiquarks. Die 91,2 GeV müssen also alleine von einem up-Quark und einem up-Antiquark aufgebracht werden. Da die Energie der Quarks in einem Protonenstrahl nicht scharf ist, sondern eine Verteilung besitzt, genügt im Experiment bereits eine Schwerpunktsenergie von über 40 GeV pro Quark bzw. Antiquark. Da aber die Energie eines Quarks nur etwa 1/6 der des Protons bzw. Antiprotons beträgt (und nicht etwa 1/3 wie man erwarten würde), muss das ganze Proton bzw. Antiproton jeweils mehr als 6 . 40 GeV = 240 GeV besitzen. Dementsprechend hatte der Protonenstrahl und der Antiprotonenstrahl im Experiment am Cern eine Strahlenergie von je 270 GeV. 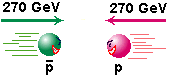(Siehe dazu auch  )