|
Elektroschwache
Vereinigung - Weinbergwinkel und die Ladungen
|
Wir kommen nun zum
Kern der elektroschwachen Vereinigung, nämlich der Darstellung des
Photons (g) und des Z0
als Mischzustände aus
B0
und W0.
Wir verwenden dazu die Schreibweise der Quantenmechanik und beschreiben
die Zustände durch ihre jeweiligen
|
Zustandsfunktionen, z.B. B0
durch YB
und W0
durch Yw.
Die Zustände YZ
und Yg
können
jeweils durch eine Linearkombination aus
YB
und YW
dargestellt werden.
|
|
Yg
=
YB
.
cosqW
+
YW
.
sinqW
YZ
=
- YB
.
sinqW
+ YW
.
cosqW
qW
nennt man den elektroschwachen Mischungswinkel
oder auch Weinberg-Winkel (vgl. mit
Cabibbo-Winkel  ). ).
Die Linearkombinationen lassen sich übersichtlicher
auch in Vektor- bzw. Matrixform schreiben:
|
(
|
Yg
|
) |
=
|
(
|
cosqW
|
sinqW
|
) |
.
|
(
|
YB
|
) |
|
YZ
|
- sinqW
|
cosqW
|
YW
|
Geometrisch bedeutet die
Multiplikation des Vektors (YB,
YW)
mit der 2 x 2-Matrix eine Drehung des
Vektors um den Winkel qW.
Zwischen
dem Weinberg-Winkel qW
und den drei Ladungen e, g und g' herrschen folgende Zusammenhänge:
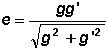 (1);
(1); 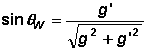 (2);
(2); 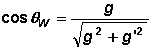 (3);
(3);
|
Die in obigen
Linearkombinationen verwendeten Sinus- und Kosinusglieder
hätte man natürlich auch gleich durch die Gleichungen (2) und (3) ersetzen
|
können.
Üblicherweise benutzt man aber wegen der besseren Übersichtlichkeit
die angegebene Schreibweise mit sinqW und
cosqW.
|
|
Setzt man (2) in (1) ein,
erhält man folgenden, zentralen Zusammenhang:
e
= g . sinqW
Welche
wichtigen Aussagen man aus diesem einfachen Zusammenhang zwischen elektrischer
und schwacher Ladung gewinnen kann, besprechen wir auf der nächsten Seite.
|
 ).
).
