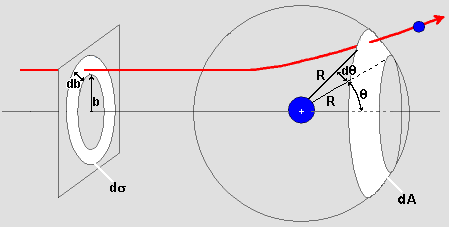
Streu-Experimente - Der differentielle Wirkungsquerschnitt bei Coulomb-Streuung   Wie groß ist der differentielle Wirkungsquerschnitt (D(q) = ds/dW) bei Coulomb-Streuung?  Wir erinnern uns an die Definition des differentiellen Wirkungsquerschnitts:   D(q) = ds/dW ist der Quotient aus   "Eintrittsflächen- und Raumwinkelelement". Wir müssen also ds und dW berechnen.   Dazu betrachten wir die rechte Abbildung:  Fliegt ein Teilchen durch den linken weißen Ring (Fläche ds), wird es so gestreut wird, dass es durch den rechten weißen "Ring" (Fläche dA, Raumwinkelelement dW = dA/R2) auf der Kugeloberfläche tritt. Wir drücken die Flächeninhalte der beiden Ringe durch die in der Abbildung angegebenen Größen aus.  ds: Die Fläche des linken Rings ist einfach "Umfang 2pb mal Breite db": ds = 2pb . db  dA: Auch hier ist die Fläche wieder "Umfang 2pR sinq mal Breite R dq", man muss nur berücksichtigen, dass sich der Ring im Abstand R vom Mittelpunkt befindet: dA = 2pR sinq . R dq  Mit dW = dA/R2 folgt: dW = 2p sinq . dq   Wir können nun den Quotienten ds/dW bilden: 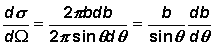  Da für wachsendes b der Streuwinkel q kleiner wird, müssen wir noch ein Minuszeichen einfügen: 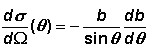    (1)  Die Größe db/dq ist die Ableitung von b nach q .   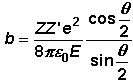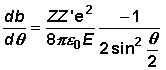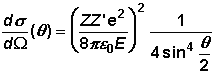Mit    folgt nach Anwendung der Quotientenregel:    (2)  (2) in (1) eingesetzt ergibt:    Hierbei wurde sinq durch 2cos(q/2)sin(q/2) (Additionstheorem) ersetzt. Der Ausdruck ist als Rutherfordsche Streuformel bekannt.  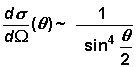Das entscheidende Ergebnis ist: Der differentielle Wirkungsquerschnitt bei Coulomb-Streuung ist proportional zu "sin-4 des halben Streuwinkels":   Man beachte hierbei, dass die Rutherfordsche Streuformel auf mehreren idealisierenden Annahmen beruht: Die Streuteilchen sind punktförmig. Zur Beschreibung der Streuung wird nur das radialsymmetrische Coulomb-Potenzial eines Streuzentrums betrachtet. Die negative elektrische Ladung der Elektronenhülle wird vernachlässigt. Es können beliebig große Stoßparameter autreten. Es tritt nur Einfachstreuung auf. Zu kleinen Streuwinkeln hin stellt man Abweichungen zwischen Experiment und der Vorhersage durch die Streuformel fest. Hier werden die Stoßparameter so groß, dass der Einfluss der Elektronen nicht mehr vernachlässigt werden kann. Weiterhin können die Stoßparameter in der Realität nicht beliebig groß werden. Sie sind durch den halben Abstand zwischen zwei Streuzentren im Target beschränkt (sog. "halbe Gitterkonstante" bei Festkörpern). Interpretation: Rechts ist die Proportionalität grafisch dargestellt. Man kann daran ablesen, wie häufig die unterschiedlichen Streuwinkel auftreten. Der Graph hat bei q = 180° ein Minimum, d.h. in Rückrichtung wird am seltensten gestreut. Sehr wahrscheinlich sind hingegen Streuwinkel um 0° also Streuungen mit sehr kleinen Ablenkungen aus der ursprünglichen Flugrichtung. Der steile Abfall des Graphen zur Mitte hin zeigt, dass die Wahrscheinlichkeit für das Auftreten größerer Streuwinkel sehr schnell abnimmt. 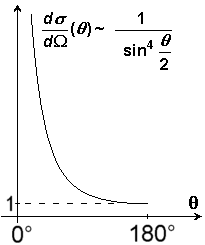Aus der Abweichung seiner Messergebnisse von diesem Verlauf für große Streuwinkel bzw. kleine Stoßparameter (ca. 10-14m) hat Rutherford (richtig) geschlossen, dass die Ausdehnung des Atomkerns wohl in dieser Größenordnung liegt.