Streuexperimente
- Der Formfaktor
|
Der
Mott-Wirkungsquerschnitt beschreibt die Streuung der Elektronen immer noch
unter der (natürlich falschen) Voraussetzung, dass es sich um punktförmige
Targets handelt. Wenn man für eine bekannte Situation (Elektron auf
Target) den Mott-Wirkungsquerschnitt berechnet und ihn mit dem experimentellen
Wirkungsquerschnitt vergleicht, stellt man Unterschiede fest. Die Unterschiede
zwischen Experiment und Mott-Theorie hängen offensichtlich vom Impulsübertrag
|q|, den das Elektron an das Target abgibt, ab. Für hohe Impulsüberträge
|q| an ausgedehnte
|
Targets wie Atomkerne oder Nukleonen ist der experimentelle Wirkungsquerschnitt kleiner. Die Wellenlänge
des Photons, das für den Impulsübertrag sorgt, wird mit steigendem
|q| kleiner und das Auflösungsvermögen entsprechend größer.
Das Elektron "sieht schärfer" und daher die Ladung des Kerns nicht mehr als ein Ganzes, sondern
einzelne, kleinere Ladungen in verschiedenen Abständen zu ihm. Der Wirkungs- querschnitt wird - der scheinbar
kleineren Targetladung entsprechend - kleiner.
|
|
 Welche
Aussagen über die Targetform kann man aus diesen Unterschieden erhalten?
Welche
Aussagen über die Targetform kann man aus diesen Unterschieden erhalten?
Die Antwort auf diese Frage ist einfach, sie bedarf lediglich
einer kurzen Vorbemerkung.
Die
"Form" eines Targets, die ein anfliegendes Elektron "sieht", wird durch
die Verteilung seiner elektrischen Ladung bestimmt. Diese Ladungsverteilung
des Targets wird durch eine Ladungs- Verteilungsfunktion r ausgedrückt
(anschaulich: r drückt
die "Ladung Z.e
|
pro Volumen V" in Abhängigkeit vom Ort
x aus; x ist hier der Ortsvektor). Der Einfachheit halber benutzt man anstelle von
r die
normierte Verteilungs- funktion f mit r(x)
= Z.e . f(x). Als einfaches Beispiel
einer normierten, radialsymmetrischen Verteilungsfunktion betrachten wir eine Kugel mit homogener
Ladungsdichte. f ist innerhalb der Kugel gleich einer Konstante
ungleich null und außerhalb gleich null. R ist der Radius der Kugel.
|
|
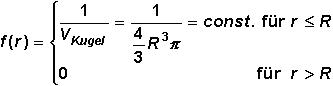
|
Das
Entscheidende ist nun, dass sich die Streuung eines Elektrons an einem
ausgedehnten geladenen Target quantenmechanisch durch die Streuung einer
ebenen Welle an einer ausgedehnten Ladungsverteilung beschreiben lässt.
Hierbei taucht ein Faktor auf, der sich für die Beschreibung der "Form"
des Targets eignet. Man nennt ihn daher auch Formfaktor F. Er hängt
vom Impulsübertrag q ab: F(q).
Seine genauere quantenmechanische Bedeutung
würde an dieser Stelle zu weit führen. Wir beschränken uns
auf folgende Sichtweise:
|
 Der
Formfaktor F(q) beschreibt die "Form" eines ausgedehnten Targets. Er hängt
vom Impulsübertrag q und der Ladungsverteilung f des Targets ab. Der
Formfaktor F(q) beschreibt die "Form" eines ausgedehnten Targets. Er hängt
vom Impulsübertrag q und der Ladungsverteilung f des Targets ab.
Da es bei radialsymmetrischen Systemen keine Unterschiede zwischen verschiedenen Richtungen
gibt, hängt der Formfaktor F
nur vom Betrag von q, also |q| ab. Da q ein Vektor ist, ist sein Betrag gleich der Wurzel aus q2.
Um auszudrücken, dass ein Formfaktor nur vom Betrag von q abhängt schreibt man üblicherweise F(q2)
anstelle von F(q).
|
|
Die Antwort auf die Frage, wie man aus den experimentell
festgestellten Unterschieden zwischen Mott`schem und experimentellem Wirkungs- querschnitt
(Exp) eine Aussage über die Targetform erhält, ist nun leicht
zu geben, denn für das Betragsquadrat des Formfaktors gilt:

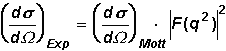
|
|F(q2)|2
ist also im Prinzip ein "Korrekturfaktor"
für den Mottschen Wirkungsquerschnitt,
der eine audgedehnte Ladungsverteilung beschreibt.
In
der Praxis bestimmt man den experimentellen Wirkungsquerschnitt und teilt
ihn durch den Mott`schen. Man erhält daraus den Betrag des Formfaktors
und entsprechende Informationen über die Ladungsverteilung des Targets.
|
|
 Die
hier beschriebenen Untersuchungen gelten nur für elastische
Streuung und solange Die
hier beschriebenen Untersuchungen gelten nur für elastische
Streuung und solange
Z.a
<< 1
erfüllt ist (also z.B. für nicht zu große Kernladungszahlen Z).
Mit ihnen lassen sich beispielsweise die Radien von Atomkernen bestimmen.
Die
Formfaktoren von Nukleonen sind
|
schwieriger zu bestimmen, da hier noch
zusätzlich die Wechselwirkung zwischen dem magnetischen Moment des
Nukleons und dem "Strom", den das sich bewegende Elektron darstellt, berücksichtigt
werden muss.
(siehe dazu auch ![zum Literaturverzeichnis; [POV 1994, S. 60 ff]](../button_gifs/booksm.gif) und
und ![zum Literaturverzeichnis; [FRA 1987, S. 140 ff]](../button_gifs/booksm.gif) ) )
|
|
Auf der letzten Seite dieses Kapitels
betrachten wir in einer Übersicht wichtige Beispiele von Formfaktoren
und ihren zugehörigen Ladungsverteilungen.
|