|
Elektromagnetische
WW - fundamentale Eigenschaften
|
Im Unterschied zur
schwachen und starken Wechselwirkung ist die elektromagnetische aufgrund
ihrer unendlichen Reichweite sowohl für Vorgänge des makroskopischen
als auch des mikroskopischen Bereich
der Teilchenphysik verantwortlich. Sowohl der Blitz bei einem Gewitter
als auch die Absorption eines g-Quants durch das Elektron einer Atomhülle
beruhen auf einer elektromagnetischen
|
Wechselwirkung. Wir wollen uns hier
zunächst einen Überblick über elektromagnetische Prozesse
verschaffen. Da wir uns mit der Teilchenphysik beschäftigen, sollen
makroskopische elektromagnetische Phänomene ausgeklammert bleiben.
Alle makroskopischen Phänomene können auf elementare Prozesse
auf Teilchenebene zurückgeführt werden.
|
|
Beispiele fundamentaler
elektromagnetischer Prozesse sind:
Anziehung und Abstoßung elektrisch geladener Teilchen
gebundene und angeregte Zustände
elektrisch geladener Teilchen, z.B. die stabile Bindung zwischen Kern und Elektron beim Wasserstoffatom
Coulomb-Streuung
Paarvernichtung und -erzeugung
Alle
elektromagnetischen Prozesse lassen sind auf einen fundamentalen Wechselwirkungsprozess
(siehe Abb. rechts) zurückführen bzw. sind aus mehreren solchen
Prozessen zusammengesetzt.
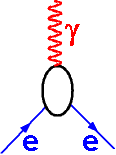
In dem dargestellten
Prozess läuft ein
|
elektrisch geladenes Teilchen
e (z.B. ein Elektron, ein geladenes Lepton
oder ein Quark) ein. An einem Wechselwirkungspunkt, der noch verdeckt (0)
dargestellt ist, emittiert oder
absorbiert das Teilchen ein
Photon (g)
und läuft wieder aus.
|
|
|
In der Teilchenphysik werden Wechselwirkungsprozesse grafisch
mit sog. Feynman-Diagrammen dargestellt,
die die Grundlage für die Berechnung von Lebensdauern, Zerfallszeiten
etc. bilden. Wir beschreiben die
|
Feynman-Diagramme erst in einem späteren
Kapitel 
zusammen mit den zugehörigen Rechenvorschriften, dem sog. Feynman-Kalkül.
|
|
|
