leptonische elektromagnetische Prozesse (Streuung)

Elektromagnetische WW - leptonische elektromagnetische Prozesse

Im folgenden betrachten wir eine Reihe von elektromagnetischen Prozessen, die nur zwischen Leptonen stattfinden. Die bei diesen Prozessen als Austauschteilchen beteiligten Photonen können als virtuelle Photonen auftreten, sie erscheinen dann nicht in der

zugehörigen Reaktionsgleichung. Reelle Photonen hingegen sind in den Reaktionsgleichungen enthalten. Die Darstellung der Prozesse erfolgt mit Feynman-Diagrammen, wobei die Zeitachse von links nach rechts (à) verläuft.

Wer mit dieser Form der Darstellung noch nicht vertraut ist, sollte sich zuerst die ersten Seiten des Kapitels über Feynman-Diagramme durchlesen

Wir beschränken uns bei jedem Beispiel auf ein Feynman-Diagramm zweiter Ordnung (d.h. Diagramm mit zwei Wechselwirkungspunkten, sog. Vertices).

MÆller-Streuung (Elektron-Elektron-Streuung)
e^- + e^- à e^- + e^-
In der klassischen Elektrodynamik nennt man die Streuung zweier elektrisch geladener Teilchen Coulomb-Streuung. Dabei sind die Wirkungsquerschnitte für Elektron-Elektron- und Elektron-

Positron-Streuung gleich

.
In der QED sind die Wirkungsquerschnitte unterschiedlich und die Prozesse werden deutlich unterschieden. Bei Elektron-Elektron- Streuung spricht man von MÆller-Streuung

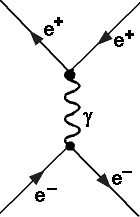
Bhabha-Streuung (Elektron-Positron-Streuung)
e^- + e⁺ à e^- + e⁺
Die Wirkungsquerschnitte von e^- + e^- und e^- + e⁺ sind in der QED verschieden! Die Streuung von Elektron und Positron wird daher in der QED einzeln, getrennt von Elektron- Elektron-Streuung betrachtet, man nennt sie Bhabha-Streuung, nach dem Physiker Bhabha (siehe Abb.).

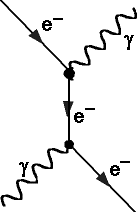
Compton-Streuung (Elektron-Photon-Streuung) e^- + g à e^- + g Unter dem "Compton-Effekt" versteht man die Streuung von Photonen (z.B. Röntgenquanten) an (quasi-) freien Elektronen. Im Originalexperiment von Arthur Holly Compton (Nobelpreis 1927) wurde kurzwelliges Röntgenlicht auf die schwach gebundenen (quasifreien) Außenelektronen von Graphit "geschossen". Energie- und Impulsübertrag bzw. die damit verbundenen Streurichtungen von Elektron und Photon lassen sich dabei wie bei einem klassischen Teilchenstoß
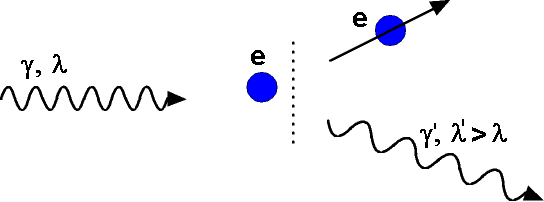
		beschreiben. Das nach dem Stoß vorhandene Photon besitzt eine größere Wellenlänge (l' > l), d.h. eine kleinere Quantenenergie als vorher. Untenstehende Abbildung zeigt den Prozess symbolisch vor und nach der Streuung. Rechts ist das entsprechende Feynman-Diagramm abgebildet.

Gamma-Quant wird an einem (quasi-) freien Elektron gestreut

Die Wellenlängendifferenz (Dl = l' - l) ist unabhängig von der ursprünglichen Wellenlänge l. Der Compton-Effekt bestätigte Einsteins Lichtquanten- hypothese, die bis dahin sehr umstritten war.

In der QED bezeichnet man Streuprozesse zwischen (auch hochenergetischen!) Elektronen und Photonen als Compton-Streuung. Die Compton-Streuung ist spinabhängig.

Mit folgendem Applet lässt sich der Compton-Effekt mit unterschiedlichen Wellenlängen simulieren. Drückt man den "Start"-Button, so erreicht eine elektromagnetische Welle das Elektron von links. Man kann die Wellenlänge auswählen. Liegt sie im sichtbaren Bereich, so kann sie stufenlos verändert werden. Die eingezeichnete Streurichtung des Elektrons ist willkürlich gewählt und hat nur symbolische Bedeutung. Mit einem verschiebbaren Detektor kann man die Wellenlänge der gestreuten Welle unter einem beliebig einstellbaren		Streuwinkel messen. Man beachte, dass zu jedem Streuwinkel ein Elektron gehört, dass unter einem zugehörigen Winkel gestreut wurde und nicht etwa das eingezeichnete Elektron. Die detektierte Wellenlänge wird in einem Koordinatensystem (rechts) über dem Streuwinkel angetragen. Gleichzeitig wird in dieser Auswertung die ursprüngliche Wellenlänge angezeigt. Man vergleiche die relative Wellenlängenverschiebungen der drei wählbaren Strahlungsarten. Unter dem Applet findet man zwei Fragen, die mit dessen beantwortet werden können.

1. Für welche Strahlung ist die absolute Wellenlängenverschiebung am größten? Für sichtbares Licht Für Gammastrahlung Sie ist für beide gleich.	2. Unter welchen Streuwinkeln findet man die größte Wellenlängenverschiebung? Bei 0° Bei +90° und -90° Bei +180° und -180°

zu 1:	zu 2:

Beispiel:
Am HERA-Speicherring bei DESY treffen Photonen eines Argon-Lasers
(l = 514 nm, E = 2,4 eV) frontal auf Elektronen (E = 26,67 GeV).

Man benutzt dabei die Spinabhängigkeit der Compton-Streuung zur Messung der Spinpolarisation der Elektronen.
(siehe

)

(siehe auch

)