Die starke Wechselwirkung - Reichweite der starken Wechselwirkung Welche Reichweiten haben Wechselwirkungen bzw. die daraus resultierenden Kräfte? Die Reichweite x einer Wechselwirkung wird man in der Regel so festlegen, dass x die maximal mögliche Entfernung zwischen zwei Teilchen ist, so dass sie gerade noch wechselwirken können. Im makroskopischen Bereich, dessen Dynamik im wesentlichen durch die elektromagnetische Wechselwirkung und die Gravitation bestimmt ist, ist diese Definition relativ unproblematisch. Man kennt die genauen Verläufe der Potenziale bzw. 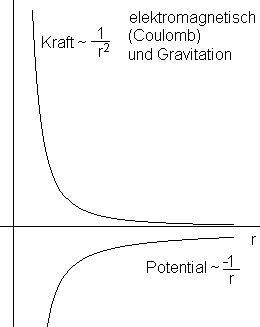der zugehörigen Kräfte und kann so sehr genau entscheiden, wie groß sie in einer bestimmten Entfernung sind. Wichtig ist dabei, dass das Coulomb-Gesetz und das Newtonsche Gravitationgesetz dieselbe Abstandsabhängigkeit besitzen. (siehe Abb. rechts und ) Beide Wechselwirkungen bzw. Kräfte haben eine unendliche Reichweite.  Welche Reichweite hat die starke Wechselwirkung zwischen Quarks, die sich auf die Größenordnung der Nukleonen (fm = 10-15 m) zu beschränken scheint? Wir wissen, dass sich die Quarks in einem Nukleon, z.B. im Proton, relativ frei bewegen können (asymptotische Freiheit). Wenn man allerdings versucht, die Quarks zu trennen, stellt man fest, dass die Kraft, die sie zusammenhält, mit steigendem Abstand sehr groß wird und einem festen Wert zustrebt. Einer vom Abstand unabhängigen, konstanten Kraft liegt ein Potenzial zugrunde, das linear mit dem Abstand ansteigt. Die Energie E, die zur Trennung der Quarks nötig ist, steigt mit größer werdendem Abstand r dementsprechend zuerst "langsam", dann annähernd linear an (in etwa nach E = kr, d.h. proportional zum Abstand r; k = const.). Bereits bei Abständen ab wenigen fm ist die nötige Energie so groß, dass sich neue Quark-Antiquark-Paare bilden und sich mit den Quarks, die man versucht zu trennen, zu neuen Hadronen zusammenschließen (Confinement). 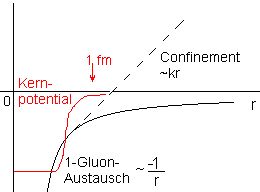Wenn man diesem Verlauf ein Potenzial zugrunde legt, hätte es (grob vereinfacht) den rechts oben abgebildeten Verlauf. Bei kleinen Abständen (< 1 fm) führt der 1-Gluon-Austausch zwischen den Quarks zu einem Potenzialverlauf, wie bei der elektromagnetischen Wechselwirkung (~ -1/r; durchgezogene Linie, schwarz). Je näher der Abstand der Größenordnung 1 fm kommt, desto mehr weicht der Verlauf vom -1/r-Potenzial ab und geht in einen linearen Verlauf (gestrichelt) über. Der rote Pfeil kennzeichnet in etwa die Stelle, an der die Energie so groß ist, dass sich neue Quark-Antiquark-Paare bilden (Größenordnung fm). Würde dies nicht geschehen, kann man vermuten, dass der lineare Anstieg des Potenzials weitergeht. Leider wird man das nie überprüfen können, da das Confinement eine unüberwindliche Hürde zu sein scheint. Insofern ist es zwar theoretisch richtig, der starken Wechselwirkung eine unendliche Reichweite zuzuschreiben, praktisch aber sinnlos, da sie für Abstände deutlich größer als der Protonendurchmesser (etwa 1 fm) keine Wirkung mehr zeigt. Aus diesem Grund gilt die starke Wechselwirkung als kurzreichweitig. Ihre Reichweite wird üblicherweise mit 1 fm, also 1.10-15 m angegeben. In obiger Grafik ist neben dem Potenzial der starken Wechselwirkung zwischen Quarks auch der Verlauf des Kernpotenzials (rot) skizziert. Der Verlauf des Kernpotenzials bestimmt die Energieniveaus der Nukleonen bzw. die Energie, die notwendig ist, Nukleonen vom Kern zu trennen. Man beachte, dass die vertikale Energieskala für die beiden Potenziale (roter und schwarzer Graph) unterschiedlich ist. Die Bestimmung des genauen Potenzialverlaufs der starken Wechselwirkung kann experimentell geschehen. Eine Möglichkeit hierzu bieten die Termschemata. Die Quantenmechanik erlaubt, bei bekanntem Potenzial die zugehörigen Energieniveaus eines gebundenen Systems zu berechnen. Umgekehrt lassen sich auch aus dem Wissen über viele Energieniveaus eines gebundenen Systems Rückschlüsse auf den zugehörigen Potenzialverlauf ziehen. Auf diese Weise wurden die Verläufe verschiedener gebundener Systeme aus Quarks (Mesonen und Baryonen), wie z.B. die des Y-Mesons (Charmonium) untersucht. (siehe dazu  und  )